Sieder-Tate Equation Calculator for Nusselt Number and Heat Transfer Coefficient

The Sieder-Tate Equation is an empirical correlation used in heat transfer to calculate Convective Heat Transfer Coefficient for fluid flow inside pipes or ducts.

The Sieder-Tate equation is a modified Dittus-Boelter equation and used for situations where fluid viscosity strongly depends on temperature, typically when the temperature difference is large between the bulk of the fluid and the surface to obtain accurate heat transfer calculations.

Related: Nusselt Number Calculator – Significance and Calculation

Sieder-Tate Equation

\[Nu = 0.027 Re^{0.8} Pr^{0.33} \left(\frac{\mu}{\mu_w}\right)^{0.14}\]

where,

• Nu is the Nusselt number, which represents the ratio of convective to conductive heat transfer across the boundary layer.
• Re is the Reynolds number, which represents the ratio of inertial forces to viscous forces in the flow.
• Pr is the Prandtl number, which represents the ratio of momentum diffusivity to thermal diffusivity.
• μ is the fluid viscosity at bulk temperature
• μ_w is the fluid viscosity at wall temperature

Note: The Sieder-Tate Correlation is valid for turbulent flow (when Re ≥ 10,000) and Prandtl Number Range (0.7 ≤ Pr ≤ 16,700) and having L/D ≥ 10.

Related: Convective Heat Transfer Calculator – Newton’s law of cooling

Related: Reynolds Number Calculator for a Circular Pipe

Sieder-Tate Equation Calculator

This Sieder-Tate Equation Calculator helps user to calculate the Convective Heat Transfer Coefficient and the Nusselt Number. It requires input values of Reynolds number, Prandtl number, and fluid viscosities at bulk and surface temperatures.

Related: Heat and Mass Transfer – Analogy and Correlations for Chemical Engineers

Related: Dittus-Boelter Equation Calculation for Turbulent Flow in Tubes

Sieder-Tate Equation Assumptions

• The flow must be fully developed, both hydrodynamically and thermally i.e velocity and temperature profiles do not change along the flow direction.
• The Sieder-Tate equation assumes constant fluid properties such as thermal conductivity, and specific heat except fluid viscosity.
• The pipe or duct surface is assumed to be hydraulically smooth.
• This equation assumes that the fluid is in a single-phase state (liquid or gas)

Note: When the Sieder-Tate equation isn’t suitable, other correlations are used to estimate the heat transfer coefficient under certain conditions.

The Dittus-Boelter equation is used in case of small to moderate temperature differences but it assumes the viscosity to be constant over entire temperature range

Related: Visit our Dittus-Boelter Equation Solver for quick calculations

The Sieder-Tate and Dittus-Boelter correlations are somewhat simplified and used certain conditions, they may produce errors of up to 25%. Therefore, using more modern correlation can reduce the error to less than 10%. Gnielinski correlation is one of such correlations.

The Gnielinski equation is used for turbulent flow in both smooth and rough pipes, as well as transitional flow, because it effectively considers surface roughness and friction effects.

\[Nu = \frac{\left(\frac{f}{8}\right)(Re – 1000)Pr}{1 + 12.7 \sqrt{\frac{f}{8}} \left(Pr^{0.66} – 1\right)}\]

where, f is the Darcy friction factor

Related: Thermal Boundary Layer Thickness (δT) for Flat Plate

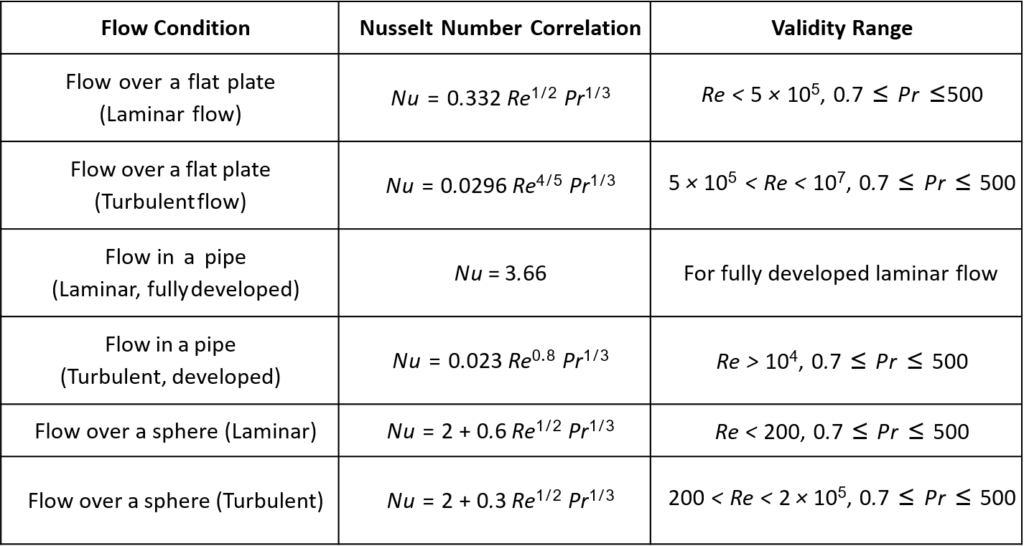
Nusselt Number Correlations

Nusselt Number is correlated with other dimensionless numbers Reynolds number (Re) and the Prandtl number (Pr) , which characterize the heat transfer processes.

Here, we have summarized Nu correlations of flow over a flat plate, within pipes, and spheres within both laminar and turbulent regimes by their validity ranges based on both Reynolds and Prandtl numbers.

Also Read: 10 Mostly used Dimensionless Numbers in Chemical Engineering

Also Read: Critical Thickness of Insulation Calculator for Cylinder and Sphere

Example Problem on Sieder-Tate Correlation

Use the Sieder-Tate equation to determine the inside heat transfer coefficient for a fluid flowing inside a 16 ft long, (1-in tube 14 BWG) at a velocity of 2.5 ft/s that is being cooled and has an average temperature of 176°F and an average wall temperature of 104°F. Consider the following fluids:

1. Acetone (liquid)
2. Isopropanol (liquid)

Use the following data:

For (1) ρ = 44.80 lbm/ft³, Cp = 0.5706 Btu/ lbm^◦F, μ at 176 ^◦F= 1.339*10^-41bm/ft, at 104 ^◦F= 1.806*10^-41bm/ft s, k = 0.0838 Btu/hrft^◦F.

For (2) ρ = 45.27 lbm/ft³, C_p = 0.8037 Btu/ lbmF, μ at 176 ^◦F = 3.55*10^-41bm/ft, μ at 104 ^◦F= 9.123*10^-41bm/ft s, k = 0.0708 Btu/hrft^◦F

Solution:

From the data given we will be solving Reynolds Number and Prandtl Number using the formula:

For quick calculation you can use our reynolds number calculator and Prandtl Number Calculator

Re = (ρ * u * D) / μ

Pr = (μ * Cp) / k

h = (Nu * k) / D

For ease of calculation, we will be using python for solving the same

# Define a function to calculate heat transfer coefficient using Sieder-Tate equation
def calculate_heat_transfer_coefficient(fluid_properties):
    # Extract fluid properties
    rho = fluid_properties['rho']
    Cp = fluid_properties['Cp']
    mu = fluid_properties['mu']
    mu_s = fluid_properties['mu_s']
    k = fluid_properties['k']
    u = fluid_properties['u']
    D = fluid_properties['D']

    # Calculate Reynolds number
    Re = (rho * u * D) / mu

    # Calculate Prandtl number
    Pr = (mu * Cp) / k

    # Calculate Nusselt number using Sieder-Tate equation
    Nu = 0.027 * (Re**0.8) * (Pr**(0.33)) * ((mu / mu_s)**0.14)

    # Calculate heat transfer coefficient
    h = (Nu * k) / D

    return h, Re, Pr, Nu

# Define fluid properties for Acetone and Isopropanol
acetone_properties = {
    'rho': 44.80,        # lbm/ft^3
    'Cp': 0.5706,        # Btu/lbm°F
    'mu': 1.339e-4,      # lbm/ft·s (bulk)
    'mu_s': 1.806e-4,    # lbm/ft·s (surface)
    'k': 0.0838,         # Btu/hr·ft°F
    'u': 2.5,            # ft/s
    'D': 0.0833          # ft (inner diameter)
}

isopropanol_properties = {
    'rho': 45.27,        # lbm/ft^3
    'Cp': 0.8037,        # Btu/lbm°F
    'mu': 3.550e-4,      # lbm/ft·s (bulk)
    'mu_s': 9.123e-4,    # lbm/ft·s (surface)
    'k': 0.0708,         # Btu/hr·ft°F
    'u': 2.5,            # ft/s
    'D': 0.0833          # ft (inner diameter)
}

# Calculate results for Acetone and Isopropanol
acetone_results = calculate_heat_transfer_coefficient(acetone_properties)
isopropanol_results = calculate_heat_transfer_coefficient(isopropanol_properties)

# Print results
print("Results:")
print("Acetone:")
print(f"  Heat Transfer Coefficient (h): {acetone_results[0]:.2f} Btu/hr·ft²°F")
print(f"  Reynolds Number (Re): {acetone_results[1]:.2f}")
print(f"  Prandtl Number (Pr): {acetone_results[2]:.5f}")
print(f"  Nusselt Number (Nu): {acetone_results[3]:.2f}")

print("\nIsopropanol:")
print(f"  Heat Transfer Coefficient (h): {isopropanol_results[0]:.2f} Btu/hr·ft²°F")
print(f"  Reynolds Number (Re): {isopropanol_results[1]:.2f}")
print(f"  Prandtl Number (Pr): {isopropanol_results[2]:.5f}")
print(f"  Nusselt Number (Nu): {isopropanol_results[3]:.2f}")

Output:

Acetone:
  Heat Transfer Coefficient (h): 19.36 Btu/hr·ft²°F
  Reynolds Number (Re): 69675.88
  Prandtl Number (Pr): 0.00091
  Nusselt Number (Nu): 19.25

Isopropanol:
  Heat Transfer Coefficient (h): 11.28 Btu/hr·ft²°F
  Reynolds Number (Re): 26556.27
  Prandtl Number (Pr): 0.00403
  Nusselt Number (Nu): 13.28

Therefore, Heat Transfer Coefficient (h) for acetone and Isopropanol is 19.36 Btu/hr·ft²°F and 11.28 Btu/hr·ft²°F respectively.

User can also validate the results of Nusselt number and heat transfer coefficient from our Sieder-Tate Equation Calculator

Also Read: Heat Transfer through Conduction Calculator – Fourier’s law 

Also Read: Hydraulic Diameter Calculator for Circular and Non-Circular cross-section

Resources

• Heat Transfer a Practical Approach – Book by Yunus A Çengel
• Industrial Chemical Process Design, 2nd Edition – Douglas L. Erwin, P.E
• “Heat Transfer Book” by David W. Hahn.
• “Introduction to Heat Transfer” by Frank P. Incropera, David P. DeWitt, Theodore L. Bergman, and Adrienne S. Lavine.

Disclaimer: The content provided here is for educational purposes. While efforts ensure accuracy, results may not always reflect real-world scenarios. Verify results with other sources and consult professionals for critical applications. Contact us for any suggestions or corrections.