Table of Contents
Heat transfer through conduction is a fundamental process that occurs when thermal energy flows through a solid material due to a temperature difference. It plays an important role in everyday life, from cooking food on a stove to maintaining comfortable indoor temperatures with insulated walls and others.
What is Thermal Conduction and Thermal Conductivity?
Heat conduction is a process in which heat energy transfers from a region of higher temperature to a region of lower temperature within a material or between different materials in direct contact. It occurs due to the random motion of atoms and molecules within a substance.
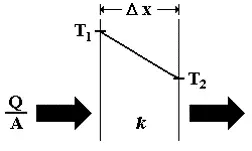
Fourier’s law, named after the French mathematician Joseph Fourier, describes the rate at which heat is conducted through a solid material.
Fourier’s Law of thermal conduction states that the rate of heat transfer (𝑄) through a material is directly proportional to the temperature gradient (𝑑𝑇/𝑑𝑥), which is the change in temperature (𝑑𝑇) per unit distance (𝑑𝑥) perpendicular to the direction of heat flow.
Mathematically, Fourier’s law can be expressed as:
𝑄 = −𝑘 𝐴 (𝑑𝑇 / 𝑑𝑥)
Where:
- 𝑄 is the rate of heat transfer (in watts or joules per second),
- 𝑘 is the thermal conductivity of the material (in watts per meter per Kelvin),
- 𝐴 is the cross-sectional area through which heat is transferred (in square meters),
- 𝑑𝑇/𝑑𝑥 is the temperature gradient (in Kelvin per meter).
In simpler terms, Fourier’s law tells us that the greater the temperature difference between two points in a material and the higher the thermal conductivity of the material, the faster heat will flow between those points.
Related: Heat Transfer through Convection Calculator – Newton’s Law of Cooling
Related: Joule-Thomson Effect – Coefficient Calculation for CO2 and N2
Heat Conduction Fourier’s Law Assumptions
- Steady-state conditions i.e no change in temperature over time.
- Material properties, such as thermal conductivity, are assumed to be uniform.
- The material is assumed to conduct heat equally in all directions.
- Effects of radiation and convection are neglected.
- Internal heat generation within the solid are negligible.
Heat Transfer through Conduction Calculator
This heat transfer through conduction calculator simplifies heat transfer calculations in solid materials, this tool uses Fourier’s law to quickly compute heat transfer rates based on parameters like thermal conductivity, thickness, and temperatures.
Related: Overall Heat Transfer Coefficient Calculator for Composite Walls
Related: Hydraulic Diameter Calculator for Circular and Non-Circular cross-section
Example Problem on Fourier’s Law of Thermal Conduction
A steel plate of thermal conductivity 50 W/m-K and thickness 10 cm passes a heat flux by conduction of 25 kW/m2. If the temperature of the hot surface of the plate is 100°C then what is the temperature of the cooler side of the plate?
Given:
- k = 50 W/m-K
- Q = 25 kW/m^2 = 25000 W/m2
- d = 10 cm = 0.1 m
- T1 = 100°C = 373.15 K (temperature of the hot surface)
We need to find T2, the temperature of the cooler side of the plate.
First, let’s rearrange Fourier’s law to solve for ΔT:
ΔT = -Q * d / (k * A)
To simplify calculations, let’s assume the plate has a square cross-section, so A equals the area of one side of the plate.
Given that A = side^2, and the thickness d, the area A is 0.1 m × 0.1 m = 0.01 m2.
Now, substitute the values into the equation:
ΔT = -(25000 W/m^2 × 0.1 m) / (50 W/m-K × 0.01 m^2)
ΔT = -(50/2500) K
ΔT = -50 K
The negative sign indicates that the temperature decreases from the hot side to the cooler side.
Finally, calculate the temperature of the cooler side:
T2 = T1 + ΔT
T2 = 373.15 K – 50 K
T2 = 323.15 K
Converting this temperature back to Celsius:
T2 = 323.15 K ≈ 50.15°C
So, the temperature of the cooler side of the plate is approximately 50.15°C.
Related: Biot Number Calculator – Significance and Calculations
Related: Critical Thickness of Insulation Calculator for Cylinder and Sphere
Python Code for Heat Transfer through Conduction
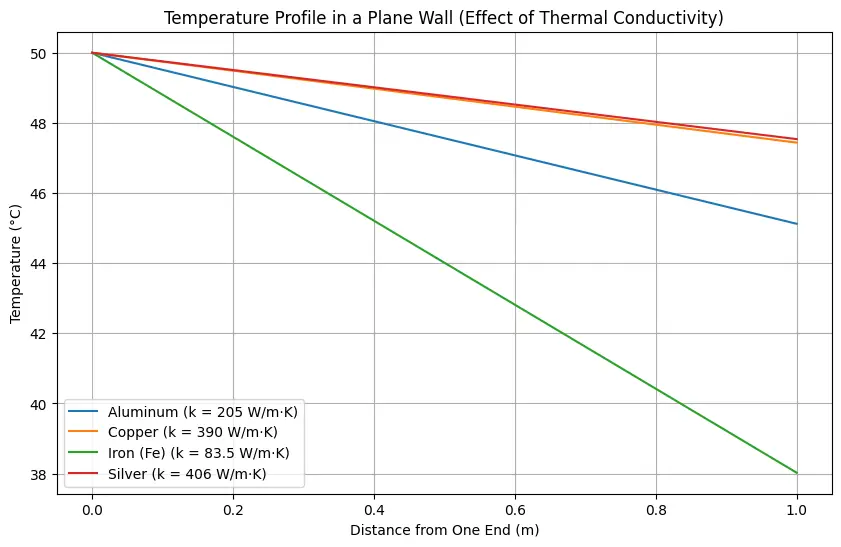
This python code for heat transfer through conduction calculates the temperature at different distances from one end of a wall. It generates temperature profiles for various materials with given thermal conductivities and plots these temperature profiles against the distance, showing how thermal conductivity impacts temperature distribution within the wall.
Note: This Python code solves the specified problem. Users can copy the code and run it in a suitable Python environment. By adjusting the input parameters, users can observe how the output changes accordingly.
"""
Calculates the temperature at a distance 'x' from one end of the wall.
x (float): Distance from one end of the wall (0 <= x <= L).
T1 (float): Initial temperature at one end (°C).
Q (float): Heat transfer rate (W).
k (float): Thermal conductivity of the material (W/m·K).
A (float): Cross-sectional area of the wall (m²).
Returns:
float: Temperature at distance 'x'.
"""
import numpy as np
import matplotlib.pyplot as plt
def temperature_profile(x, T1, Q, k, A):
return T1 - (Q / (k * A)) * x
# Example parameters
L = 1.0 # Wall thickness (m)
T1 = 50.0 # Initial temperature at one end (°C)
Q = 500.0 # Heat transfer rate (W)
A = 0.5 # Cross-sectional area (m²)
# Thermal conductivities (W/m·K)
k_aluminum = 205.0
k_copper = 390.0
k_iron = 83.5
k_silver = 406.0
# Generate x values
x_values = np.linspace(0, L, num=100)
# Calculate temperatures for each material
temperatures_aluminum = temperature_profile(x_values, T1, Q, k_aluminum, A)
temperatures_copper = temperature_profile(x_values, T1, Q, k_copper, A)
temperatures_iron = temperature_profile(x_values, T1, Q, k_iron, A)
temperatures_silver = temperature_profile(x_values, T1, Q, k_silver, A)
# Create the plot
plt.figure(figsize=(10, 6))
plt.plot(x_values, temperatures_aluminum, label="Aluminum (k = 205 W/m·K)")
plt.plot(x_values, temperatures_copper, label="Copper (k = 390 W/m·K)")
plt.plot(x_values, temperatures_iron, label="Iron (Fe) (k = 83.5 W/m·K)")
plt.plot(x_values, temperatures_silver, label="Silver (k = 406 W/m·K)")
plt.xlabel("Distance from One End (m)")
plt.ylabel("Temperature (°C)")
plt.title("Temperature Profile in a Plane Wall (Effect of Thermal Conductivity)")
plt.grid(True)
plt.legend()
plt.show()Output:
Resources
- Heat Transfer a Practical Approach – Book by Yunus A Çengel
- “Fundamentals of Heat and Mass Transfer” by Theodore L. Bergman, Adrienne S. Lavine, Frank P. Incropera, and David P. DeWitt.
- “Heat Transfer Book” by David W. Hahn.
- “Conduction of Heat in Solids” by H.S. Carslaw and J.C. Jaeger.
- “Introduction to Heat Transfer” by Frank P. Incropera, David P. DeWitt, Theodore L. Bergman, and Adrienne S. Lavine.
Disclaimer: The Solver provided here is for educational purposes. While efforts ensure accuracy, results may not always reflect real-world scenarios. Verify results with other sources and consult professionals for critical applications. Contact us for any suggestions or corrections.