Table of Contents
Heat Exchangers are essential in many industries, it helps to transfer heat between fluids at different temperatures. Effectiveness – NTU (Number of Transfer Units) and LMTD (Log Mean Temperature Difference) methods are widely used in the heat exchanger analysis.
LMTD method are used when the fluid inlet temperatures are known and the outlet temperatures are specified or readily determined from the energy balance expressions. If only inlet temperatures are known, the method becomes iterative and cumbersome, it makes the effectiveness-NTU method a better alternative.
Also Read: Van der Waals Equation Calculator and PV Isotherm for Real Gases
Effectiveness – NTU Calculator
This Effectiveness – NTU Calculator for Heat Exchanger Analysis helps user to compute the NTU, effectiveness, Heat Capacity Ratio, heat transfer rate, heat exchanger area or Overall heat transfer coefficient based on the user input.
Input the values for Hot and Cold Fluid and then it measures the area of heat exchanger based on given value for overall heat transfer coeffcient (U) for the selected type of heat exchanger (e.g parallel flow, counterflow, shell-and-tube, cross flow).
Note: This calculator allow user to adjust inlet and outlet temperatures to see the effect on heat exchanger performance. By changing parameters, users can see how temperature changes affect the heat exchanger area, heat duty, and other parameters like effectiveness and NTU.
Related: LMTD Calculator with correction factor for Heat Exchanger Design
Related: Heat Transfer through Conduction Calculator – Fourier’s law
What is Effectiveness – NTU Method
The Effectiveness (ε) – NTU (Number of Transfer Unit) method is widely used approach for heat exchanger analysis where the outlet temperatures are unknown. It relates the performance of the heat exchanger to its physical characterstics and operating conditions.
Effectiveness (ε) for a heat exchanger is defined as the ratio of the actual heat transfer rate (qactual) to the maximum possible heat transfer rate (qmax). Effectiveness formula is written as:
\[\varepsilon = \frac{q_{\text{actual}}}{q_{\text{max}}}\]
The maximum heat transfer occurs when the fluid with the minimum heat capacity experiences the maximum temperature change.
qmax = Cmin . ΔTmax
where:
- ΔTmax = | Th,in−Tc,in | is the maximum possible temperature difference between the hot and cold fluid.
- Cmin = min (Ch ,Cc) is the smaller heat capacity rate of the two fluids (Ch=mhcp,h , Cc=mccp,c).
Therefore, the formula for effectiveness, the actual heat transfer rate can be defined as:
qactual = ε . min (Ch ,Cc) . (Th,in−Tc,in)
Number of Transfer Units (NTU) is defined as dimensionless parameter which represents the size and efficiency of the heat exchanger relative to the heat capacity rate of the fluid with Cmin. Mathematically, NTU is written as:
\[\text{NTU} = \frac{U A}{C_{\text{min}}}\]
where:
- U is the overall heat transfer coefficient (W/m2. K)
- A is the heat transfer surface area (m2)
- Cmin is the minimum heat capacity rate (W/K)
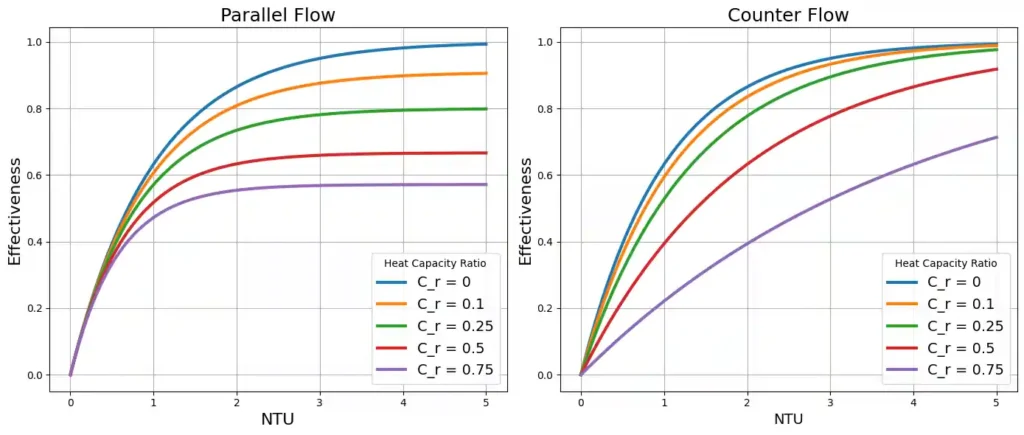
For any heat exchanger effectiveness, ε is a function of NTU and Heat Capacity Ratio, Cr = Cmin/Cmax i.e ε = f ( NTU, Cr )
How to Calculate NTU & Effectiveness
To calculate the NTU & effectiveness we will follow the steps given here:
Step 1. Calculate the maximum possible heat transfer (qmax) and the actual heat transfer (q) based on fluid properties and flow rates.
Step 2. Calculate the heat capacity ratio, Cr=Cmin/Cmax
Step 3. Find effectiveness (ε) using the formula ε=q/qmax
Step 4. Determine NTU for the calculated value of ε and Cr
For the given type of heat exchanger, there is a relationship between NTU & effectiveness or we can calculate it with the help of charts provided for different type of heat exchangers.
| Type of Heat Exchanger | Formula | Additional |
|---|---|---|
| Parallel Flow | \[NTU = \frac{-\ln(1 – \varepsilon \cdot (1 + C_r))}{1 + C_r}\] | – |
| Counter Flow (for Cr<1) | \[NTU = \frac{1}{C_r – 1} \ln\left(\frac{\varepsilon – 1}{\varepsilon C_r – 1}\right)\] | – |
| Counter Flow (for Cr=1) | \[NTU = \frac{\varepsilon}{1 – \varepsilon}\] | – |
| Shell and Tube (One Shell Pass and 2, 4, … Tube Passes) | \[NTU_1 = -A^{-\frac{1}{2}} \cdot \ln\left(\frac{E – 1}{E + 1}\right)\] | \[A = 1 + C_r^2\] \[E = \frac{2 / \varepsilon_1 – (1 + C_r)}{(1 + C_r^2)^{\frac{1}{2}}}\] \[\varepsilon_1 = \frac{F – 1}{F – C_r}\] |
| Shell and Tube (n Shell Passes and 2n, 4n, … Tube Passes) | \[NTU = n \cdot NTU_1\] | \[F = \left(\frac{\varepsilon C_r – 1}{\varepsilon – 1}\right)^{\frac{1}{n}}\] |
| Cross Flow (Cmax Mixed, Cmin Unmixed) | \[NTU = -\ln\left(1 + \frac{B}{C_r}\right)\] | \[B = \ln(1 – \varepsilon C_r)\] |
| Cross Flow (Cmax Unmixed, Cmin Mixed) | \[NTU = \frac{-1}{C_r} \ln(C_r D + 1)\] | \[D = \ln(1 – \varepsilon)\] |
Table Source: “Introduction to Heat Transfer” by Frank P. Incropera, David P. DeWitt, Theodore L. Bergman, and Adrienne S. Lavine.
Once you know the values of NTU and ε then you can determine the heat exchanger area or Overall heat transfer coefficient, Therefore, it will help user to design the Heat Exchanger.
Related: Online Psychrometric Calculator for Chemical Engineers
Example Problem on Effectiveness – NTU
Water (CP = 4180 J/kg.◦C) is to be heated by solar-heated hot air (CP = 1010 J/kg.◦C) in a double-pipe counter flow heat exchanger. Air
enters the heat exchanger at 90◦C at a rate of 0.3 kg/s while water enters at 22◦C at a rate of 0.1 kg/s. The overall heat transfer coefficient based on the inner side of the tube is given to be 80 W/m2.◦C. The length of the tube is 12 m and the inner diameter of the tube is 1.2 cm. Determine the outlet temperature of the water and the air.
Given Data: Double-Pipe Counter Flow Heat Exchanger
- Cold fluid: water, CPc = 4180 J/kg.◦C, m˙c = 0.1 kg/s , Th,in = 22◦C ,
- Hot fluid: air, CPh = 1010 J/kg.◦C, m˙h = 0.3 kg/s, Tc,in = 90◦C
- Heat Transfer Area, A = πDL = 3.142 × 0.012 × 12 = 0.4524 m2
- Overall heat transfer coefficient (U) : 80 W/m²·°C
To Find: Th,out & Tc,out
To solve this question we will be using ε-NTU method, we wil follow the step given in this article:
Step 1. Calculate the heat capacity ratio, Cr and NTU from the given information
Cair = ˙mhCPh = 0.3 × 1010 = 303 W/◦C = Cmin
Cwater = ˙mcCPc = 0.1 × 4180 = 418 W/◦C = Cmax
Cr = Cmin / Cmax = 303/ 428 = 0.725
From the definition of NTU
NTU = UA/ Cmin = (80 × 0.4524)/303 = 0.12
We get the values, for Cr = 0.725 & NTU = 0.12
Step 2. Calculate the ε value form the chart or relationship given for counter flow heat exchanger, using relation:
\(\varepsilon = \frac{1 – \exp(-NTU \cdot (1 – C_r))}{1 – C_r \cdot \exp(-NTU \cdot (1 – C_r))}\)
Substituting the values, we get
\(\varepsilon = \frac{1 – \exp\left(-0.12 \cdot (1 – 0.725)\right)}{1 – 0.725 \cdot \exp\left(-0.12 \cdot (1 – 0.725)\right)}\)
ε = 0.109
Step 3. Calculate the Heat transfer rate
q = ε . qmax = ε Cmin (Th,in − Tc,in)
q = 0.109 × 0.303 × (90 − 22) = 2246 W
Step 4. Calculation of outlet temperatures
Using the energy balance, q = m˙c . CPc . (Tc,out – Tc,in ) = m˙h . CPh . (Th,in – Th,out )
On rearranging, we get Tc,out = Tc,in + q/m˙cCPc
Tc,out = 22 + 2246/0.1 × 4180 = 27.4 ◦C
On rerranging, we get Th,out = Th,in − q/m˙hCPh
Th,out = 90 − 2246/0.3 × 1010 = 82.6 ◦C
Therefore, the Th,out & Tc,out values are 82.6 ◦C & 27.4 ◦C respectively.
Edition: 9th Edition, By: Don W. Green, Marylee Z. Southard
The ultimate resource for chemical engineering, covering core concepts, data, and insights. An invaluable reference for students, engineers, and industry professionals.
Buy on AmazonRelated: LMTD Calculator with correction factor for Heat Exchanger Design
Resources
- Heat Transfer a Practical Approach – Book by Yunus A Çengel
- Industrial Chemical Process Design, 2nd Edition – Douglas L. Erwin, P.E
- “Heat Transfer Book” by David W. Hahn.
- “Introduction to Heat Transfer” by Frank P. Incropera, David P. DeWitt, Theodore L. Bergman, and Adrienne S. Lavine.
Disclaimer: The content provided here is for educational purposes. While efforts ensure accuracy, results may not always reflect real-world scenarios. Verify results with other sources and consult professionals for critical applications. Contact us for any suggestions or corrections.