Table of Contents
In heat transfer processes, the concept of critical thickness of insulation or critical radius of insulation plays an important role in heat transfer optimization. In general adding more insulation to a outer surface always decreases heat transfer. The thicker the insulation, the lower the heat transfer rate but to a certain extent.
In this article, we will describe a Critical Thickness of Insulation Calculator for Cylinders and Spheres, which is an essential tool for engineers and designers. This calculator helps in determining the optimal insulation thickness required to minimize heat transfer without compromising system efficiency.
Related: Nusselt Number Calculator – Significance and Calculation
What is Critical Thickness of Insulation?
The critical thickness of insulation is a concept in heat transfer, it is the specific thickness of an insulating material at which the rate of heat transfer through the material is maximized.
As most of the industrial application involves cylindrical and spherical objects for example a hot water pipe (cylindrical) or a spherical storage tank. If the insulation is too thin, heat loss will be high. If the insulation is too thick, the increased surface area can lead to higher convective losses. Therefore, finding the optimum critical thickness becomes relevant to minimize overall heat transfer.
Formula for Critical Thickness of Insulation for Cylinder:
\[r_{\text{critical}} = \frac{k}{h}\]
Formula for Critical Thickness of Insulation for Sphere:
\[r_{\text{critical}} = \frac{2k}{h}\]
where in S.I. units,
- rcritical is the Critical radius of insulation (m)
- k is the thermal conductivity of insulation (W/m.K)
- h is the convective heat transfer coefficient (W/m2. K)
Related: Heat Transfer through Conduction Calculator
Related: Overall Heat Transfer Coefficient Calculator for Composite Walls
Critical Thickness of Insulation Calculator for Cylinder and Sphere
This Critical Thickness of Insulation Calculator helps users to determine the optimal thickness of insulation for either a cylindrical or spherical object. Use the slider to adjust the values of the thermal conductivity of the insulation material and the convective heat transfer coefficient.
Related: Heat Transfer Calculators for Chemical Engineering
Related: Kirchoff’s Law of Thermal Radiation, Wien’s Displacement Law
Related: Joule-Thomson Effect – Coefficient Calculation for CO2 and N2
Critical Thickness / Radius of Insulation
- The critical radius of insulation depends on the thermal conductivity of the insulation (k) and the external convection heat transfer coefficient (h).
- The rate of heat transfer from the surface increases with the addition of insulation for r2<rcr and reaches a maximum when r2= rcr and starts to decrease for r2>rcr
- Thus, insulating the pipe may actually increase the rate of heat transfer from the pipe instead of decreasing it when r2<rcr
- The additional insulation increases the conduction resistance of the insulation layer but decreases the convection resistance of the surface because of the increase in the outer surface area for convection.
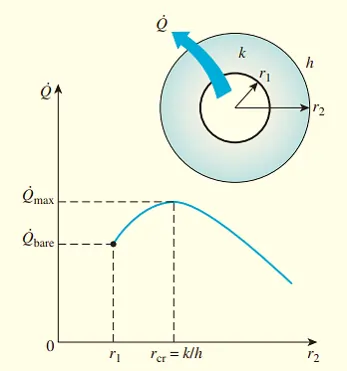
Critical Thickness of Insulation for Cylinder
For a cylindrical surface, the rate of heat transfer is the combination of conduction (through the insulation) and convection (through medium) is given by:
\[q = \frac{2 \pi L (T_1 – T_{\infty})}{\frac{\ln{\left(\frac{r_2}{r_1}\right)}}{k} + \frac{1}{h r_2}}\]
where:
- qcond is the heat transfer rate by conduction (W)
- L is the length of the cylinder (m)
- k is the thermal conductivity of the insulation material (W/mK)
- T1 is the temperature of the surface of the cylinder (K)
- T∞ is the temperature of the outer surface of the insulation (K)
- r1 is the radius of the cylinder (m)
- r2 is the outer radius of the insulation (m)
- h is the convective heat transfer coefficient (W/m2K)
To minimize heat loss, differentiate q with respect to r2 and set it equal to zero:
\[\frac{d q}{d r_2} = 0\]
Taking the derivative of the heat loss equation with respect to r2 and simplifying:
\[\frac{d}{d r_2} \left( \frac{1}{\frac{\ln{\left(\frac{r_2}{r_1}\right)}}{k} + \frac{1}{h r_2}} \right) = 0\]
Therefore, the critical radius of insulation for cylinder is:
\[r_{\text{critical}} = \frac{k}{h}\]
Related: Joule-Thomson Effect – Coefficient Calculation for CO2 and N2
Critical Thickness of Insulation for Sphere
For a spherical surface, the rate of heat transfer is the combination of conduction (through the insulation) and convection (through the medium), given by:
\[q = \frac{4 \pi r_1^2 (T_1 – T_{\infty})}{\frac{r_2 – r_1}{k r_1 r_2} + \frac{1}{h r_2^2}}\]
where:
- qcond is the heat transfer rate by conduction (W)
- L is the length of the cylinder (m)
- k is the thermal conductivity of the insulation material (W/mK)
- T1 is the temperature of the surface of the cylinder (K)
- T∞ is the temperature of the surrounding medium (K)
- r1 is the radius of the cylinder (m)
- r2 is the outer radius of the insulation (m)
- h is the convective heat transfer coefficient (W/m2K)
To minimize heat loss, differentiate q with respect to r2 and set it equal to zero:
\[\frac{d q}{d r_2} = 0\]
Taking the derivative of the heat loss equation with respect to r2 and simplifying:
\[\frac{d}{d r_2} \left( \frac{1}{\frac{r_2 – r_1}{k r_1 r_2} + \frac{1}{h r_2^2}} \right) = 0\]
Thus, the critical radius of insulation for a sphere is:
\[r_{\text{critical}} = \frac{2k}{h}\]
Related: Heat and Mass Transfer – Analogy and Correlations for Chemical Engineers
Example Problem on Critical Radius of Insulation
A 3-mm-diameter and 5-m-long electric wire is tightly wrapped with a 2-mm thick plastic cover whose thermal conductivity is k = 0.15 W/m·K. Electrical measurements indicate that a current of 10 A passes through the wire and there is a voltage drop of 8 V along the wire. If the insulated wire is exposed to a medium at T= 30°C with a heat transfer coefficient of h =12 W/m2·K as shown in figure.
Determine the temperature at the interface of the wire and the plastic cover in steady operation. Also determine the critical radius of Insulation?
Given:
Given:
- Electric Wire: Diameter: 3 mm & Length: 5 m
- Plastic Cover: Thickness: 2 mm & Thermal Conductivity (k): 0.15 W/m·K
- Current: 10 A & Voltage Drop: 8 V
- Outside Temperature (T∞) = 30°C
- Heat Transfer Coefficient (h): 12 W/m²·K
We assume one-dimensional steady state heat transfer and the thermal contact resistance at the interface is negligible.
Heat is generated uniformly throughout the wire and is transferred to the surrounding medium in the radial direction
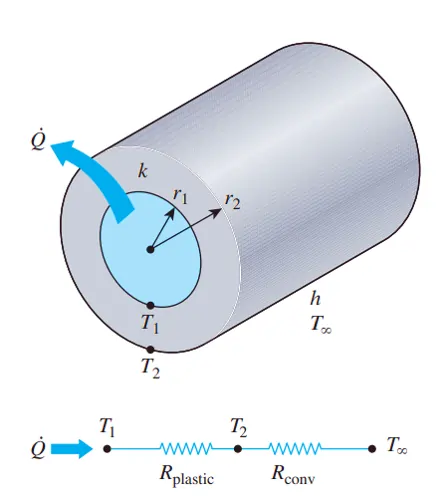
The rate of heat generation is:
\[\dot{Q} = V \cdot I = 8 \times 10 = 80 \, \text{W}\]
Now, calculating thermal resistance across the insulation thickness due to conduction and air due to convection
The surface area of the wire covered by the plastic is:
\[A_2 = 2 \pi r_2 L = 2 \pi (0.0035) (5)\]
\[A_2 = 0.110 \, \text{m}^2\]
The convective resistance is:
\[R_{\text{conv}} = \frac{1}{h A_2}\]
\[R_{\text{conv}} = \frac{1}{12 \times 0.110} = 0.76 \, \frac{K}{W}\]
The conductive resistance, where r1 and r2 are the inner and outer radius of the plastic cover
\[R_{\text{plastic}} = \frac{\ln(r_2 / r_1)}{2 \pi k L}\]
\[R_{\text{plastic}} = \frac{\ln(0.0035 / 0.0015)}{2 \pi (0.15) (5)}\]
\[R_{\text{plastic}} = 0.18 \, \frac{K}{W}\]
The total thermal resistance is:
\[R_{\text{total}} = R_{\text{conv}} + R_{\text{plastic}}\]
\[R_{\text{total}}= 0.76 + 0.18 = 0.94 \, \frac{K}{W}\]
The temperature difference between the wire surface and the ambient is:
\[\Delta T = \dot{Q} \cdot R_{\text{total}} = 80 \times 0.94\]
\[\Delta T = 75.2 ^\circ\text{C}\]
Thus, the temperature at the interface is:
\[T_{\text{interface}} = T_\infty + \Delta T \]
\[T_{\text{interface}} = 30 + 75.2 = 105^\circ\text{C}\]
Now, calculating the critical radius of insulation, using formula \(r_{\text{critical}} = \frac{k}{h}\)
\[r_{\text{cr}} = \frac{0.15}{12} = 0.0125 \, \text{m}\]
Thus, the critical radius of insulation is \(r_{\text{cr}} = 12.5 \, \text{mm}\)
Related: Hydraulic Diameter Calculator for Circular and Non-Circular cross-section
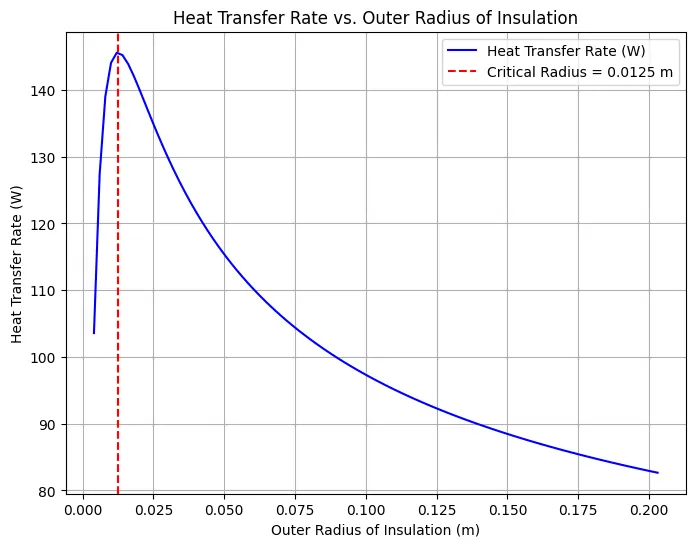
Python code for Critical Thickness of Insulation
This python code helps user to determine the critical radius of insulation and plots the heat transfer rate as a function of the outer radius of insulation for a cylindrical pipe.
Note: This Python code solves the specified problem. Users can copy the code and run it in a suitable Python environment. By adjusting the input parameters, users can observe how the output changes accordingly.
import numpy as np
import matplotlib.pyplot as plt
# Given parameters
k = .15 # Thermal conductivity of insulation material (W/m·K)
h = 12 # Convective heat transfer coefficient of surrounding medium (W/m²·K)
r1 = 0.003 # Radius of bare cylinder (m)
delta_T = 75 # Temperature difference between cylinder surface and surroundings (°C)
L = 5.0 # Length of the cylinder (m)
# Calculate the critical thickness (for a cylinder)
r_critical = k / h
print(f"Critical Radius (r_critical): {r_critical:.4f} m")
# Generate an array of outer radii (r2) values, starting from r1 to a larger radius
r2 = np.linspace(r1 + 0.001, r1 + 0.2, 100) # Range of outer radius (m)
# Calculate the total heat transfer resistance for each r2
R_insulation = np.log(r2 / r1) / (2 * np.pi * k * L) # Thermal resistance of insulation
R_convection = 1 / (2 * np.pi * h * r2 * L) # Convective resistance at the outer surface
R_total = R_insulation + R_convection # Total thermal resistance
# Calculate heat transfer rate (Q)
heat_transfer = delta_T / R_total # Heat transfer rate (W)
# Plot heat transfer rate vs outer radius
plt.figure(figsize=(8, 6))
plt.plot(r2, heat_transfer, label="Heat Transfer Rate (W)", color="b")
plt.axvline(x= r_critical, color='r', linestyle='--', label=f"Critical Radius = { r_critical:.4f} m")
plt.xlabel("Outer Radius of Insulation (m)")
plt.ylabel("Heat Transfer Rate (W)")
plt.title("Heat Transfer Rate vs. Outer Radius of Insulation")
plt.grid(True)
plt.legend()
plt.show()Output: Critical Radius (r_critical): 0.0125 m
Resources
- Heat Transfer a Practical Approach – Book by Yunus A Çengel
- “Fundamentals of Heat and Mass Transfer” by Theodore L. Bergman, Adrienne S. Lavine, Frank P. Incropera, and David P. DeWitt.
- “Heat Transfer Book” by David W. Hahn.
- “Conduction of Heat in Solids” by H.S. Carslaw and J.C. Jaeger.
- “Introduction to Heat Transfer” by Frank P. Incropera, David P. DeWitt, Theodore L. Bergman, and Adrienne S. Lavine.
Disclaimer: The Solver provided here is for educational purposes. While efforts ensure accuracy, results may not always reflect real-world scenarios. Verify results with other sources and consult professionals for critical applications. Contact us for any suggestions or corrections