Table of Contents
Thermal radiation is one of the fundamental mechanisms of heat transfer, alongside conduction and convection. Heat transfer through radiation is a process where thermal energy is emitted by a substance in the form of electromagnetic waves.
Thermal radiation transmits as an electromagnetic wave through both matter and vacuum. When matter absorbs thermal radiation its temperature will tend to rise. At room temperature, most of the thermal radiation occurs in the infrared (IR) spectrum.

For eg. The Sun emits thermal radiation, which we perceive as warmth. It’s the primary source of heat and light for our planet.
Related: Nusselt Number Calculator – Significance and Calculation
Stefan–Boltzmann law
The Stefan–Boltzmann law, also known as Stefan’s law, describes the intensity of thermal radiation emitted by matter in terms of its temperature.
It states that the total energy radiated by a blackbody (an idealized object that absorbs all radiation incident upon it) is directly proportional to the fourth power of its absolute temperature.
Mathematically, it is expressed as
\[P = \varepsilon \cdot \sigma \cdot A \cdot T^4\]
Where:
– \( P \) is the power radiated (in watts),
– \( A \) is the surface area of the object (in square meters),
– \( T \) is the absolute temperature of the object (in Kelvin),
– \( \sigma \) is the Stefan-Boltzmann constant, approximately equal to \( 5.67 \times 10^{-8} \, \text{W m}^{-2} \text{K}^{-4} \)
– \(ε\) is the emissivity of the surface, a dimensionless quantity between 0 and 1.
Related: Inverse Square Law for Radiation
Stefan–Boltzmann Law Calculator
This Stefan-Boltzmann Law Calculator is a versatile tool for computing parameters associated with blackbody radiation. Users can determine radiative power (W), emissivity (ε), and temperature (K) of a surface.
Related: Heat Transfer through Conduction Calculator
Related: Heat Transfer through Convection Calculator – Newton’s Law of Cooling
Assumptions for Stefan–Boltzmann law
- The object behaves like a blackbody, meaning it absorbs all incident radiation and emits the maximum possible amount of radiation at a given temperature. In reality, no object is a perfect blackbody, but many real objects behave similarly under certain conditions.
- The radiation emitted by the object is homogeneous, meaning it is emitted uniformly from the surface of the object.
- The object is in thermal equilibrium, meaning its temperature remains constant over time.
- There are no external factors affecting the emission and absorption of radiation, such as nearby heat sources or radiation-blocking materials.
Significance of Emissivity
Emissivity determines how effectively a material emits thermal radiation. A high emissivity means that a material emits radiation well, while a low emissivity means it emits less radiation. This property is crucial for understanding how materials exchange heat through radiation.
Example Problem on Stefan Boltzmann Law
A body of emissivity, e = 0.75, with a surface area A = 300 cm² and a temperature T = 227°C is kept in a room at a temperature of T₀ = 27°C. Using the Stefan-Boltzmann law, calculate the initial value of net power emitted by the body.
P = eσA (T⁴ – T₀⁴)
Where:
– e is the emissivity of the body (0.75)
– σ is the Stefan-Boltzmann constant (5.67 × 10⁻⁸ W/m²-K⁴)
– A is the surface area of the body (300 cm², converted to square meters: 300 × 10⁻⁴ m²)
– T is the temperature of the body in Kelvin (227°C converted to Kelvin: 500 K)
– T₀ is the temperature of the surroundings in Kelvin (27°C converted to Kelvin: 300 K)
Now, plug in these values:
P = (0.75) × (5.67 × 10⁻⁸ W/m²-K⁴) × (300 × 10⁻⁴ m²) × [(500 K)⁴ – (300 K)⁴]
P ≈ 69.4 Watts
So, the initial value of net power emitted by the body is approximately 69.4 Watts.
Related: Heat Transfer through Conduction Calculator
Related: Overall Heat Transfer Coefficient Calculator for Composite Walls
Python Code for Stefan Boltzmann Law
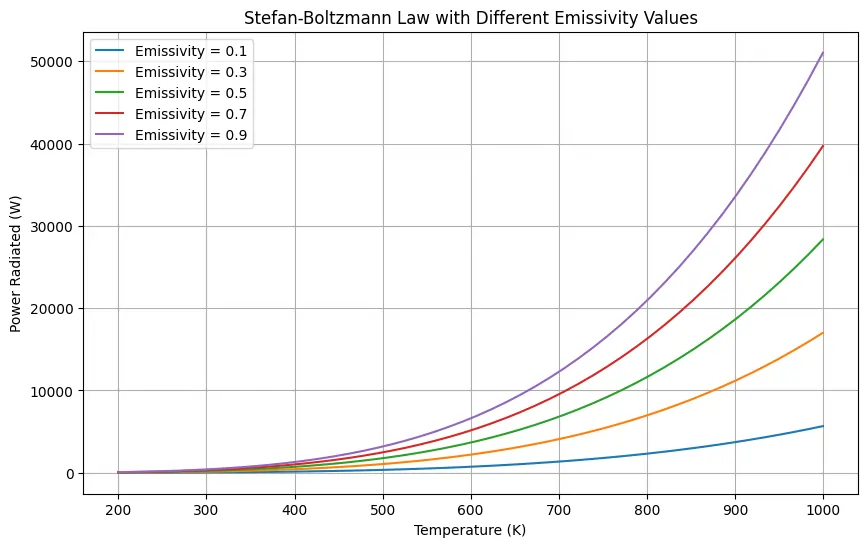
This Python code calculates and visualizes the power radiated by a black body surface according to the Stefan-Boltzmann Law. It computes the power radiated as a function of temperature, taking into account the emissivity and surface area of the body.
Note: This Python code solves the specified problem. Users can copy the code and run it in a suitable Python environment. By adjusting the input parameters, users can observe how the output changes accordingly.
import numpy as np
import matplotlib.pyplot as plt
# Constants
sigma = 5.67e-8 # Stefan-Boltzmann constant in W/m^2/K^4
# Function to calculate power radiated with emissivity
def stefan_boltzmann_emissivity(T, A, emissivity):
return emissivity * sigma * A * T**4
# Temperature range (in Kelvin)
T_range = np.linspace(200, 1000, 100)
# Surface area (in square meters)
A = 1.0 # Assuming unit area
# Emissivity values
emissivity_values = [0.1, 0.3, 0.5, 0.7, 0.9]
# Plotting
plt.figure(figsize=(10, 6))
for emissivity in emissivity_values:
power = stefan_boltzmann_emissivity(T_range, A, emissivity)
plt.plot(T_range, power, label=f'Emissivity = {emissivity}')
plt.title('Stefan-Boltzmann Law with Different Emissivity Values')
plt.xlabel('Temperature (K)')
plt.ylabel('Power Radiated (W)')
plt.grid(True)
plt.legend()
plt.show()Output:
Resources:
- “Radiative Heat Transfer” by Michael F. Modest
- “Principles of Heat Transfer” by Frank Kreith and Raj M. Manglik
- “Introduction to Heat Transfer” by Theodore L. Bergman, Adrienne S. Lavine, Frank P. Incropera, and David P. DeWitt
- “Python Documentation” – Official guides and references for Python.
Disclaimer: The Solver provided here is for educational purposes. While efforts ensure accuracy, results may not always reflect real-world scenarios. Verify results with other sources and consult professionals for critical applications. Contact us for any suggestions or corrections.