Chemical engineering is a multi disciplinary field that combines principles of chemistry, physics, mathematics, and engineering to design and operate processes that convert raw materials into valuable products. Fundamental constants are the important parameters which is used for accurate calculations and predictions.
Related: Arrhenius Activation Energy Calculator for two temperatures
These fundamental constants are also the building blocks of many scientific laws and equations that describe the behavior of chemical systems. For example, Arrhenius Equation \(\left(k = A e^{-\frac{E_a}{RT}}\right)\), here the universal gas constant R determines how temperature affects the rate of a chemical reaction.
Related: Chemical Engineering as a career option in India

Here in this article we will discuss top 15 Fundamental Constants Every Chemical Engineer Should Know. These constants are essential for a wide range of calculations in chemical engineering, including thermodynamics, fluid mechanics, heat transfer, and reaction kinetics.
Related: Importance of Programming and Coding in Chemical Engineering
Fundamental Constants
Universal Gas Constant (R)
The Universal Gas Constant, denoted by \(R\), is a fundamental constant that relates the energy scale to the temperature scale in the ideal gas law. It is a proportionality constant that relates the pressure, volume, and temperature of an ideal gas.
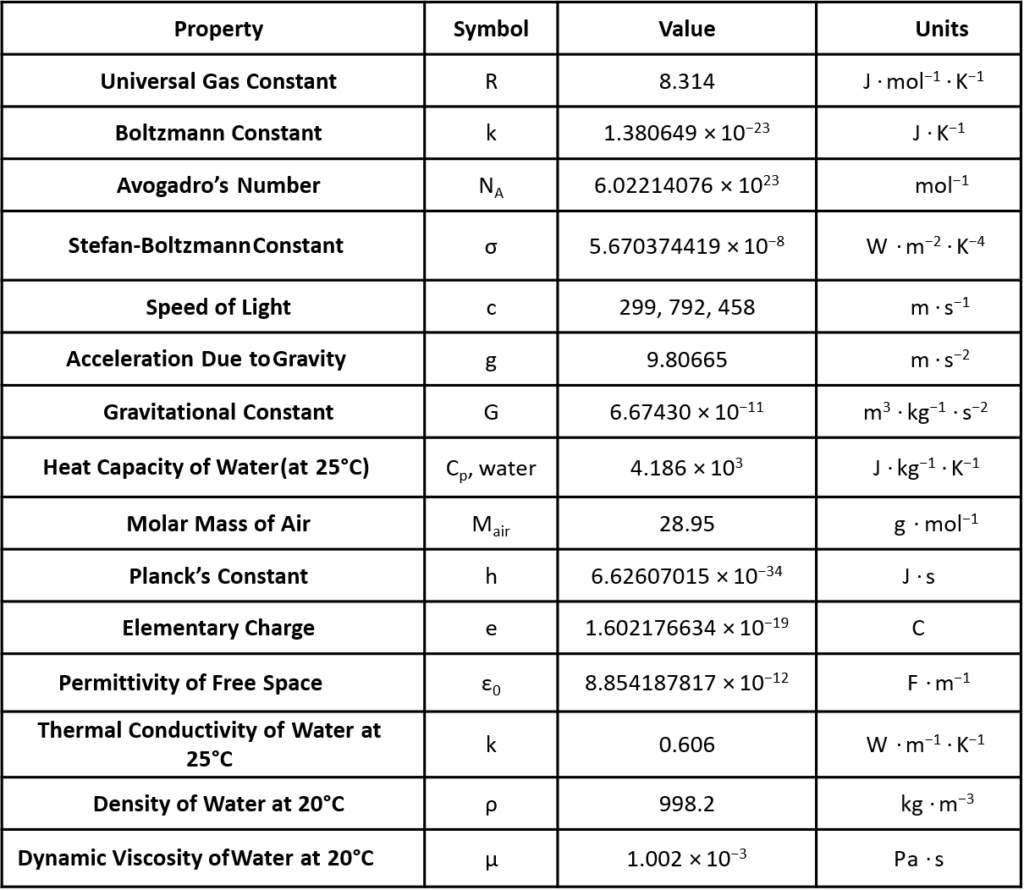
Value of R with units:
- R = 8.314 \( \text{J}\ / ( \text{mol} \cdot \text{K} ) \)
- R = 0.0821 \( \text{L} \cdot \text{atm}\ /(\text{mol} \cdot \text{K}) \)
- R = 8.314 x 107 \(\text{erg}/(\text{mol} \cdot \text{K}) \)
- R = 1.987 \( \text{cal}/(\text{mol} \cdot \text{K}) \)
In Thermodynamics, R is used in the derivation of other important equations and concepts, such as the derivation of the specific heats of gases, entropy, and Gibbs free energy.
Also Read: Joule-Thomson Effect – Coefficient Calculation for CO2 and N2
In chemical process simulations and modeling software like Aspen Plus or HYSYS, \(R\) is embedded in various calculations to predict the behavior of gases in reactors, separators, and pipelines.
Edition: Revised 2nd Edition, By: R. Byron Bird, Warren E. Stewart, Edwin N. Lightfoot
Comprehensive coverage of transport phenomena, including momentum, heat, and mass transfer. Updated content for better clarity.
Buy on AmazonBoltzmann Constant (k)
The Boltzmann Constant, denoted by \(\text{k}\), is a fundamental constant that links the average kinetic energy of particles in a gas to the temperature of the gas.
Mathematically, it is defined as the ratio of the Universal Gas Constant \(R\) to Avogadro’s number \(N_A\):
\[k = \frac{R}{N_A}\]
Boltzmann Constant appears in the relationship between the energy of particles and temperature, in the equation:
\[\langle E_{\text{kin}} \rangle = \frac{3}{2} kT\]
where:
- \(\langle E_{\text{kin}} \rangle \) is the average kinetic energy of a particle,
- \(\text{k}\) is the Boltzmann Constant,
- \(T\) is the absolute temperature (in Kelvin).
The Boltzmann Constant value is used in statistical mechanics and thermodynamics, it connects macroscopic thermodynamic quantities (like temperature) to microscopic properties (like the kinetic energy of individual particles).
Related: Arrhenius Activation Energy Calculator for two temperatures
value of \(\text{k}\) with units
- \(k = 1.380649 \times 10^{-23} \, \text{J/K}\)
- \(k = 8.617333262 \times 10^{-5} \, \text{eV/K}\)
- \(k = 1.380649 \times 10^{-16} \, \text{erg/K}\)
In chemical engineering, \(\text{k}\) is important for understanding and modeling the behavior of gases, reaction kinetics, and heat capacities at the molecular level.
Also Read: Rate Constant Calculation for Zeroth, First and Second Order using Integrated Rate Equations
Avogadro’s Number \(N_A\)
Avogadro’s Number, denoted by \(N_A), is the number of atoms, molecules, or particles contained in one mole of a substance. This number is helpful measuring the quantities as the microscopic level.
Mathematically, it is defined as:
\(N_A\)=6.02214076×1023 particles/mol
This fundamental constant indicates that one mole of any substance contains exactly 6.02214076×1023 entities, whether they are atoms, molecules, ions, or other particles.
Also Read: 10 Mostly used Dimensionless Numbers in Chemical Engineering
Avogadro’s Number is essential in stoichiometric calculations, which involve the relationships between the quantities of reactants and products in chemical reactions.
Stefan-Boltzmann Constant (σ)
The Stefan-Boltzmann Constant, denoted by \(\sigma\), is a fundamental constant that appears in the Stefan-Boltzmann law, which describes the power radiated by a black body in terms of its temperature. The Stefan-Boltzmann law is expressed as:
\[P = \varepsilon \cdot \sigma \cdot A \cdot T^4\]
Where:
– \( P \) is the power radiated (in watts),
– \( A \) is the surface area of the object (in square meters),
– \( T \) is the absolute temperature of the object (in Kelvin),
– \( \sigma \) is the Stefan-Boltzmann constant
– \(ε\) is the emissivity of the surface, value range between 0 and 1.
The constant \(\sigma\) represents the proportionality factor that relates the temperature of a black body to the radiant energy it emits.
Value of \(\sigma\) are:
\(\sigma = 5.670374419 \times 10^{-8} \, \frac{\text{W}}{\text{m}^2 \, \text{K}^4}\)
\(\sigma = 5.670374419 \times 10^{-5} \, \frac{\text{erg}}{\text{cm}^2 \, \text{s} \, \text{K}^4}\)
\(\sigma = 5.670374419 \times 10^{-8} \, \frac{\text{J}}{\text{s} \, \text{m}^2 \, \text{K}^4}\)
In Heat Transfer, Stefan-Boltzmann Constant is vital in the study of radiation heat transfer, particularly in systems where high temperatures are involved, such as furnaces, boilers, and heat exchangers.
Related: Kirchoff’s Law of Thermal Radiation, Wien’s Displacement Law
Related: Joule-Thomson Effect – Coefficient Calculation for CO2 and N2
Edition: 9th Edition, By: Don W. Green, Marylee Z. Southard
The ultimate resource for chemical engineering, covering core concepts, data, and insights. An invaluable reference for students, engineers, and industry professionals.
Buy on AmazonSpeed of Light (c)
The speed of light, denoted by c, is a fundamental constant which represents the speed at which light travels in a vacuum. It is one of the most important constants in engineering and has a fixed value defined by the International System of Units (SI).
Mathematically, it is expressed as:
\[c = 299{,}792{,}458 \, \frac{\text{m}}{\text{s}}\]
This constant not only represents the speed of electromagnetic waves (such as light) in a vacuum but also plays a crucial role in the theory of relativity, where it relates space and time.
Value of speed of light in other units:
- \(c = 2.99 \times 10^{10} \, \frac{\text{cm}}{\text{s}}\)
- \(c = 299{,}792.458 \, \frac{\text{km}}{\text{s}}\)
- \(c = 9.836 \times 10^{-7} \, \frac{\text{ft}}{\text{ns}}\)
- \(c = 186{,}282 \, \frac{\text{miles}}{\text{s}}\)
In quantum chemistry and molecular physics, the speed of light directly affects the energy calculations for photons, affecting reaction kinetics, molecular transitions, and thermal radiation processes.
Edition: 3rd Edition, By: Octave Levenspiel
A classic textbook covering the principles of chemical reaction engineering with detailed analysis of reactor design and kinetics.
Buy on AmazonAcceleration Due to Gravity (g)
Acceleration due to gravity is the acceleration that an object experiences due to the gravitational pull of the Earth. It is fundamental constant which is used in the design and analysis of processes involving fluid flow, separation processes, and mechanical equipment such as pumps and compressors.
value of g with units are:
- \(g = 9.80665 \, \text{m/s}^2\)
- \(g = 980.665 \, \text{cm/s}^2\)
- \(g = 32.174 \, \text{ft/s}^2\)
- \(g = 9.80665 \, \text{N/kg}\)
In chemical engineering, g is used in fluid dynamics, determining pressure drops in fluid systems, and designing equipment where gravitational forces influence the movement and separation of materials.
Related: Hagen-Poiseuille Equation Calculator
Gravitational Constant (G)
The gravitational constant, denoted by G, is a fundamental constant used in physics in the equation for Newton’s law of universal gravitation. In Newton’s law, the force of gravity F between two masses \(m_1\) and \(m_2), separated by a distance r, is given by:
\[F = G \frac{m_1 m_2}{r^2}\]
In chemical engineering, the gravitational constant is used in understanding the gravitational forces that affect mass and fluid movement in processes.
Values of G are:
- \(G = 6.67430 \times 10^{-11} \, \frac{\text{m}^3}{\text{kg} \, \text{s}^2}\)
- \(G = 6.67430 \times 10^{-8} \, \frac{\text{cm}^3}{\text{g} \, \text{s}^2}\)
- \(G = 3.439 \times 10^{-8} \, \frac{\text{ft}^3}{\text{slug} \, \text{s}^2}\)
Related: Hydraulic Diameter Calculator for Circular and Non-Circular cross-section
Heat Capacity of Water \(C_p,water\)
The heat capacity of water at constant pressure, denoted as \(C_p, water\), is the amount of heat energy required to raise the temperature of one gram (or one mole) of water by one degree Celsius (or one Kelvin) while keeping the pressure constant. Mathematically, it is defined as:
\[C_p = \left(\frac{\partial Q}{\partial T}\right)_P\]
where:
- Q is the heat added
- T is the temperature
- P is the pressure
- \(C_p\) represents the specific heat capacity at constant pressure.
The heat capacity of water is a key parameter in designing cooling systems, such as those used in power plants, where water is used as a coolant to absorb and transfer large amounts of heat.
Related: Joule-Thomson Effect – Coefficient Calculation for CO2 and N2
Values of \(C_p, water\) are:
- \(C_p, \text{water} = 4.18 \, \frac{\text{J}}{\text{g} \cdot \text{K}}\)
- \(C_p, \text{water} = 4.18 \, \frac{\text{kJ}}{\text{kg} \cdot \text{K}}\)
- \(C_p, \text{water} = 1 \, \frac{\text{cal}}{\text{g} \cdot \text{°C}}\)
- \(C_p, \text{water} = 75.3 \, \frac{\text{J}}{\text{mol} \cdot \text{K}}\)
- \(C_p, \text{water} = 18 \, \frac{\text{Btu}}{\text{lb} \cdot \text{°F}}\)
In Chemical Engineering, heat capacity of water is a fundamental property which is used in energy balance calculations, for processes involved in heating, cooling, and phase changes of water. It helps in determining the amount of energy required to achieve a desired temperature change in water or aqueous systems.
Also Read: Antoine Equation Calculator for Vapour Pressure versus Temperature Calculations
Molar Mass of Air
The molar mass of air is the mass of one mole of air molecules, Molar mass is expressed in grams per mole (g/mol). Since air is a mixture of gases, primarily nitrogen (N2), oxygen (O2), argon (Ar), and carbon dioxide (CO2).
Its molar mass is an average value based on the composition of these gases. The standard molar mass of dry air is approximately 28.97 g/mol.
In Thermodynamics, the molar mass of air is important for calculating properties such as the specific heat, density, and viscosity of air. These properties are critical for designing equipment like heat exchangers, compressors, and turbines.
Planck’s Constant (h)
Planck’s constant, denoted by h, is a physical fundamental constant that relates the energy of a photon to its frequency. The equation is given by:
\[E = h \nu \]
where:
- E is the energy of the photon,
- \(\nu\) is the frequency of the photon,
- h is Planck’s constant.
Planck’s constant sets the scale of quantum effects and is fundamental in describing the behavior of particles at the atomic and subatomic levels.
Value of Plank’s constant, h are:
- \(h = 6.62607015 \times 10^{-34} \, \text{J} \cdot \text{s}\)
- \(h = 4.135667696 \times 10^{-15} \, \text{eV} \cdot \text{s}\)
- \(h = 6.62607015 \times 10^{-27} \, \text{erg} \cdot \text{s}\)
- \(h = 6.582119569 \times 10^{-16} \, \frac{\text{eV}}{\text{Hz}}\)
In Quantum Mechanics Planck’s constant helps in understanding how atoms and molecules absorb and emit light. This is very useful in characterizing materials, studying reaction kinetics, and designing chemical sensors.
Also Read: Rate Constant Calculation using Arrhenius Equation Calculator
Elementary Charge (e)
The elementary charge (e) is the fundamental constant unit of electric charge in the International System of Units (SI). It represents the charge of a single proton (positive) or the magnitude of the charge of a single electron (negative). This quantity is used in electromagnetism and quantum mechanics.
Value of Elementary Charge:
- \(e = 1.602176634 \times 10^{-19} \, \text{C}\)
- \(e = 1.602176634 \times 10^{-19} \, \text{As}\)
- \(e = 1.602176634 \times 10^{-19} \, \frac{\text{J}}{\text{V}}\)
- \(e = 1.602176634 \times 10^{-19} \, \text{V} \cdot \text{s}\)
In electrochemical processes, such as batteries, fuel cells, and electrolysis, the elementary charge is required for calculating the amounts of charge transferred during chemical reactions.
Also Read: Performance Equation for Ideal Batch Reactor
Also Read: Rate Constant Calculation using Arrhenius Equation Calculator
Permittivity of Free Space (ε₀)
The permittivity of free space, denoted as \(\varepsilon_0\), is a physical fundamental constant that describes the ability of a vacuum to permit the electric field lines. It is a measure of the resistance encountered when forming an electric field in a vacuum. The permittivity of free space is defined as:
\[\varepsilon_0 = \frac{1}{\mu_0 c^2}\]
where:
- \(\varepsilon_0\) is the permeability of free space,
- c is the speed of light in a vacuum.
The permittivity of free space is important in understanding the concept of electrostatic forces, molecular interactions, such as dipole-dipole interactions, ion-dipole interactions, and Coulomb’s law.
Value of Permittivity of Free Space are:
- \(\varepsilon_0 = 8.854187817 \times 10^{-12} \, \frac{\text{F}}{\text{m}}\)
- \(\varepsilon_0 = 8.854187817 \times 10^{-12} \, \frac{\text{C}^2}{\text{N} \cdot \text{m}^2}\)
- \(\varepsilon_0 = 8.854187817 \times 10^{-12} \, \frac{\text{C}^2}{\text{J} \cdot \text{m}}\)
In chemical engineering, dielectric materials are used in various applications, such as capacitors, insulators, and sensors. Relative permittivity of material are measured.
Also Read: Importance of Programming and Coding in Chemical Engineering
Also Read: Chemical Engineering as a career option in India
Thermal Conductivity of Water at 25°C
The thermal conductivity of water at 25°C is a measure of how efficiently heat is conducted through water at this temperature. It measures the rate at which heat energy is transferred through water due to a temperature gradient. The higher the thermal conductivity, the better the material is at conducting heat.
Related: Heat Transfer through Conduction Calculator
Values of Thermal Conductivity of Water at 25°C
- \(k = 0.606 \, \frac{\text{W}}{\text{m} \cdot \text{K}}\)
- \(k = 0.606 \times 10^3 \, \frac{\text{mW}}{\text{m} \cdot \text{K}}\)
- \(k = 0.606 \, \frac{\text{kcal}}{\text{h} \cdot \text{m} \cdot \text{°C}}\)
- \(k = 0.606 \, \frac{\text{BTU}}{\text{h} \cdot \text{ft} \cdot \text{°F}}\)
In Unit Operations involving interactions between water and other materials, the thermal conductivity of water affects how heat is transferred between different phases.
Also Read: Heat Transfer through Convection Calculator – Newton’s Law of Cooling
Density of Water at 20°C (ρ)
The density of water at 20°C \(\rho\) is defined as the mass of water per unit volume at this specific temperature. It is a fundamental constant used in various calculations and engineering applications. The density of water varies with temperature, and at 20°C, it is a commonly referenced value in chemical engineering.
Values of \(\rho\) at 20oC are:
- \(\rho = 0.9982 \, \frac{\text{g}}{\text{cm}^3}\)
- \(\rho = 998.2 \, \frac{\text{kg}}{\text{m}^3}\)
- \(\rho = 0.9982 \, \frac{\text{g}}{\text{mL}}\)
- \(\rho = 62.43 \, \frac{\text{lb}}{\text{ft}^3}\)
The density of water affects fluid dynamics calculations, such as flow rates, pressure drops, and Reynolds numbers. It is also used in thermodynamic calculations to determine properties like specific volume and internal energy.
Related: Newton’s Law of Viscosity Calculator – Dynamic Viscosity
Dynamic Viscosity of Water at 20°C (μ)
The dynamic viscosity of water at 20°C \(\mu\) is a measure of the fluid’s resistance to shear or flow. It quantifies how much force is required to move one layer of water relative to another layer.
Dynamic Viscosity of Water at 20°C
- \(\mu = 1.002 \, \text{mPa} \cdot \text{s}\)
- \(\mu = 1.002 \, \text{cP}\)
- \(\mu = 1.002 \times 10^{-3} \, \frac{\text{N} \cdot \text{s}}{\text{m}^2}\)
- \(\mu = 1.002 \times 10^{-3} \, \frac{\text{kg}}{\text{m} \cdot \text{s}}\)
In fluid flow calculations, viscosity is used in Reynolds numbers, pressure drops, and flow rates in pipelines and other transport systems.
Related: Reynolds Number Calculator for a Circular Pipe
These fundamental constants and properties are essential for design considerations in various chemical processes, from optimizing heat transfer and fluid dynamics to understanding material properties and reaction kinetics. Right knowledge and application of these values enable engineers to improve the process efficiency, safety, and innovation in their work.
Resources
- Introduction to Chemical Engineering (Hardcover) by C M Van ‘t Land
- CRC Handbook of Chemistry and Physics” by David R. Lide
- Perry’s Chemical Engineers’ Handbook“ by Don W. Green and Marylee Z. Southard
- “Transport Processes and Unit Operations“ by Christie J. Geankoplis
Disclaimer: The content provided here is for educational purposes. While efforts ensure accuracy, results may not always reflect real-world scenarios. Verify results with other sources and consult professionals for critical applications. Contact us for any suggestions or corrections.









