Water Density & Specific Weight Calculation – Variation with temperature and Pressure

Water is everywhere, and its behavior varies with temperature and pressure. Density indicates how much mass occupies a given volume, while specific weight reflects how heavy water feels due to gravity.

These properties are crucial for understanding water’s role in nature, engineering, and daily life. In this article, we will explore the calculations for the density and specific weight of water and how it changes with temperature and pressure.

Water Density and Specific Weight Calculator

This Water Density and Specific Weight Calculator is a web-based tool that computes the density and specific weight of water using the IAPWS-95 formulation, the international standard for water properties.

It calculates density as a function of temperature and then adjusts for pressure using water’s compressibility. The results are displayed numerically and visualized on a chart, making it useful for educational or engineering applications.

Related: Area of Cross-Section Calculator for Hollow Sections, Beams & Shapes

Related: Specific Heat Capacity Calculation for Water and Other Substances

Density and Specific Weight of water

Density (ρ) is defined as the mass of a substance per unit volume, its units are kilograms per cubic meter (kg/m³) or grams per cubic centimeter (g/cm³). It quantifies how much matter is packed into a given space, which provides the measure of compactness.

\[\rho = \frac{m}{V}\]

Density of water is 998.207 kg/m³ at 4°C under standard atmospheric pressure (1 atm). Objects with lower density float on water, while those with higher density sink.

Specific weight (γ) is the weight of a substance per unit volume, expressed in newtons per cubic meter (N/m³). It is the product of density and the acceleration due to gravity. It reflects the force exerted by gravity on the mass of the material.

\[ \gamma = \rho \cdot g \]

The specific weight of water is 9810 N/m³ calcuated as density of water multiplied by gravitational acceleration (9.81 m/s²).

Related: Newton’s Law of Viscosity Calculator – Dynamic Viscosity

Related: Hagen-Poiseuille Equation Calculator / Poiseuille’s Law Solver

Water’s Density variation with Temperature

Water shows a unique density-temperature relationship due to its molecular structure and hydrogen bonding. Water does not follow a simple linear decrease in density with increasing temperature as other substance does.

Water has a maximum density at approximately 4°C under standard atmospheric pressure, with density decreasing on either side of this point.

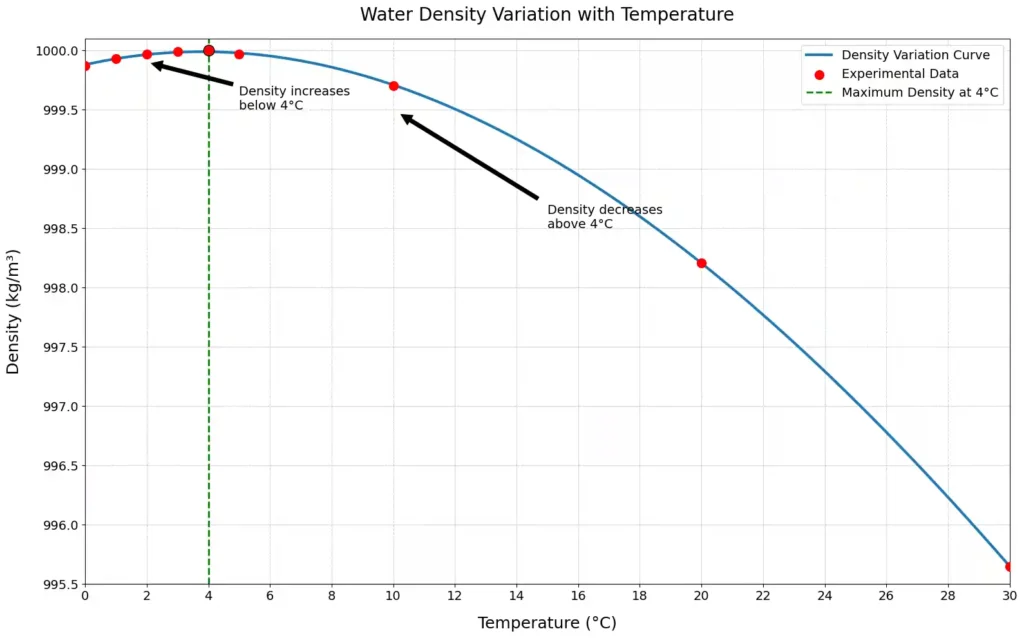
• Water’s density decreases at higher temperatures due to thermal expansion (e.g., 958.3655 kg/m³ at 100°C and 1 atm) and increases as temperature drops due to water molecules moves close together around 4°C.
• Water reaches its maximum density of 999.975 kg/m³ (≈1000 kg/m³) at 3.98°C (277.13 K) under 1 atm. At this temperature, hydrogen bonds optimize packing efficiency, resulting in the highest density.
• Below 3.98°C, water’s density decreases, for e.g., at 0°C (liquid water), it is 999.8395 kg/m³, slightly less than the maximum because hydrogen bonds begin to form a more open hexagonal structure.
• At 0°C, ice has a much lower density (≈916.7 kg/m³) than liquid water due to its open hexagonal structure, which is why ice floats on water.

Related: Reynolds Number Calculator for a Circular Pipe

Effect of Pressure on Water Density

Pressure has a significant effect on density of water, as it compresses the liquid, reducing the volume occupied by water molecules and thereby increasing density.

water is relatively incompressible compared to gases, so the change in density with pressure is small. For example, at 4°C, increasing the pressure from 1 atm to 100 atm raises the density from 999.975 kg/m³ to 1004.2 kg/m³ (IAPWS-95).

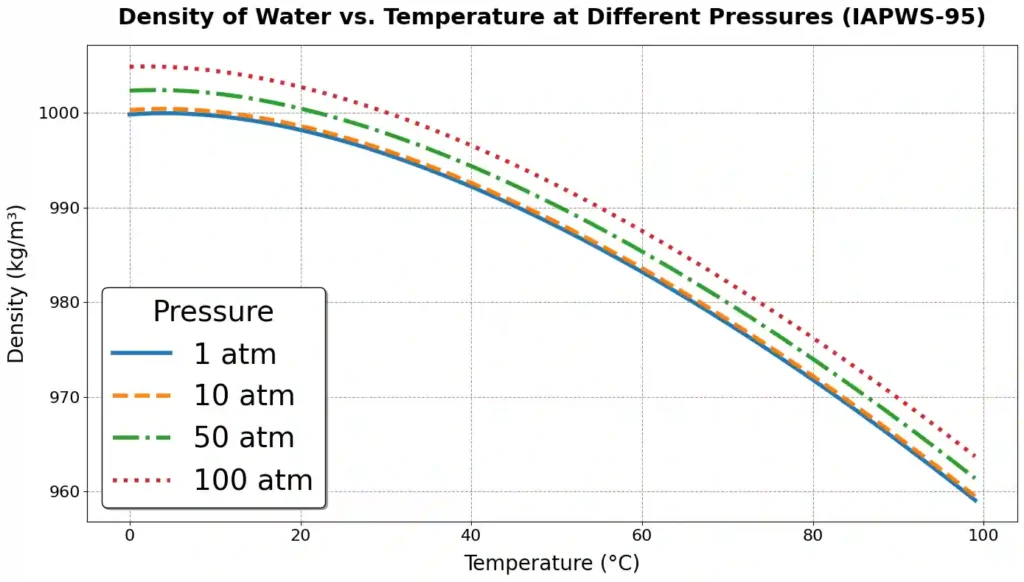
The effect of pressure on water density is usually modeled using isothermal compressibility (κ_T), which relates the change in density (Δρ) to a change in pressure (ΔP) at constant temperature. The fundamental equation is given as:

\[\kappa_T = \frac{1}{\rho} \left( \frac{\partial \rho}{\partial P} \right)_T\]

For small pressure changes, the change in density (Δρ) is approximated as:

\[\Delta \rho = \rho_0 \cdot \kappa_T \cdot \Delta P\]

where:

• ρ_o is the density at reference pressure (kg/m³)
• κ_T is the Isothermal compressibility (Pa^-1)
• ΔP = P – P_ref is pressure change from reference (Pa), with (P_ref = 0.101325 MPa)

therefore, the density at the given pressure is given by:

ρ = ρ_o + Δρ

\[\rho = \rho_0 \cdot (1 + \kappa_T \cdot \Delta P)\]

Water’s compressibility (κ_T) shows how much it shrinks under pressure. At room temperature (20°C) and normal pressure (1 atm), it’s about 4.6×10⁻¹⁰ Pa⁻¹. As temperature rises from 0°C to 100°C, κ_T increases from 4.5×10⁻¹⁰ to 5.0×10⁻¹⁰ Pa⁻¹ allows water to squeeze.

But as the pressure reaches high, like 1000 MPa, κ_T drops to around 2×10⁻¹⁰Pa⁻¹, which means it becomes difficult to compress the water. IAPWS-95 library provides the full range of accurate density values.

Also Read: Antoine Equation Calculator for Vapour Pressure versus Temperature Calculations

Also Read: Online Psychrometric Calculator for Chemical Engineers

Below is the table provided for the density and specific weight for your reference.

Source: Wagner, W., & Pruß, A. (2002). The IAPWS Formulation 1995 for the Thermodynamic Properties of Ordinary Water Substance for General and Scientific Use. Journal of Physical and Chemical Reference Data, 31(2), 387–535. https://doi.org/10.1063/1.1461829

Note: The densities and specific weights were calculated using the iapws Python library – see full python code here.

Related: Clausius Clapeyron Equation Calculator, Derivation and Applications

Related: Friction Factor Calculator Moody’s Diagram for Smooth and Rough Pipes

Resources

• “Thermodynamics: An Engineering Approach” by Yunus A. Çengel and Michael A. Boles
• “Introduction to Chemical Engineering Thermodynamics” by J.M. Smith, H.C. Van Ness, and M.M. Abbott
• NPTEL Lectures on Thermodynamics

Disclaimer: The Solver provided here is for educational purposes. While efforts ensure accuracy, results may not always reflect real-world scenarios. Verify results with other sources and consult professionals for critical applications. Contact us for any suggestions or corrections

📋 About the Authors

✍️ Written by

Nikita Aggarwal

Nikita Aggarwal is a Computer Science Engineer and co-founder of ChemEnggCalc, an engineering education platform dedicated to making chemical engineering calculations accessible to students and professionals worldwide. With over 6 years of teaching experience at ABSS Engineering College, India, she has developed a deep understanding of how engineers learn and apply technical concepts in practice. At ChemEnggCalc, Nikita leads the development of interactive calculators and digital learning tools that bridge the gap between theoretical engineering education and real-world application. Her work focuses on simplifying complex engineering methodologies into accurate, easy-to-use computational resources for the global chemical engineering community.

🔗 Author Profile 💼 LinkedIn

✅ Technically Verified by

Nitish Gupta

M.Tech Chemical Engineering | 7+ Years Experience in R&D and Process

Practicing Chemical Engineer with 7+ years of industry experience in R&D and Process. Technically verifies all calculations and engineering content on ChemEnggCalc for real-world accuracy.

🔗 Author Profile 💼 LinkedIn

✅ All calculations and technical content are verified by a qualified Chemical Engineer before publishing.