Van der Waals Equation Calculator and PV Isotherm for Real Gases

Understanding the behavior of real gases are important in the field of chemical engineering, Real gases deviate from ideal gas behavior due to the finite size of molecules and the presence of intermolecular forces. The Van der Waals Equation of State and other real gas models are useful to take care of these factors and provides more accurate description of gas behavior under non-ideal conditions.

What is Van der Waals Equation of State?

The Van der Waals Equation is first practical cubic equation of state which describes the behavior of real gases. Unlike Ideal Gas Law, this equation accounts for the finite size of molecules and the attraction between them. It provides more accurate prediction about the behavior of real gases, especially under high pressure and low temperature conditions.

The Van der Waals Equation of State is given by:

\[\left(P + \frac{an^2}{V^2}\right) (V – nb) = nRT\]

where:

• \( P \) is the pressure of the gas,
• \( V_m \) is the molar volume of the gas,
• \( T \) is the temperature,
• \(n\) is the no. of moles of gas,
• \( R \) is the universal gas constant,
• \( a \) is a measure of the attraction between particles,
• \( b \) is the volume occupied by the gas molecules.

Key Points:

• The purpose of the term \(\frac{a}{V_m^2}\) is to account for the attractive forces between molecules, which make the pressure lower than that which would be exerted in the ideal-gas state.
• The purpose of constant \(b\) is to account for the finite size of molecules, which makes the volume larger than in the ideal-gas state.

Related: Relation Between Van der Waals Constants and Critical Constants

Related: Clausius Clapeyron Equation Calculator, Derivation and Applications

Van der Waals Equation of State Calculator

This web tool is used to calculate the thermodynamic properties like Pressure, Volume, Temperature, or Number of Moles of a chemical compound based on the Van der Waals equation. The value of calculated volume is based on assumption where simplified the equation by putting the \(PV=nRT\) and converted the cubic equation into simpler form (calculation provided below).

Note: Data table for constant values (a and b) are provided in the table below, identify the chemical from the list and put the correct value of a and b.

Related: Kirchoff’s Law of Thermal Radiation, Wien’s Displacement Law

Related: Joule-Thomson Effect – Coefficient Calculation for CO2 and N2

Van der Waals Constant (a and b values) – Data Table

Here are the following table lists the Van der Waals constants for various compounds including a number of common gases and volatile liquids.

Data Source: Van der Waals constant – a and b values

Compound Name	a (Pa·m⁶/mol²)	b (m³/mol)
Xenon	0.425	0.00005105
Water	0.5536	0.00003049
Trimethylamine	1.337	0.0001101
Trifluoromethane	0.5378	0.000064
Trichloromethane	1.534	0.0001019
Toluene	2.438	0.0001463
Tin tetrachloride	2.727	0.0001642
Thiophene	1.721	0.0001058
Tetrahydrofuran	1.639	0.0001082
Tetrafluorosilane	0.5259	0.0000724
Tetrafluoromethane	0.404	0.0000633
Tetrafluoroethylene	0.6954	0.0000809
Tetrachlorosilane	2.096	0.000147
Tetrachloromethane	2.001	0.0001281
Sulfur hexafluoride	0.7857	0.0000879
Sulfur dioxide	0.6803	0.00005636
Silicon tetrafluoride	0.4251	0.00005571
Silane	0.4377	0.00005786
Radon	0.6601	0.00006239
Pyrrole	1.882	0.0001049
Pyridine	1.977	0.0001137
Propene	0.8442	0.0000824
Propane	0.8779	0.00008445
Phosphine	0.4692	0.00005156
Phenol	2.293	0.0001177
Pentane	1.926	0.000146
Ozone	0.357	0.0000487
Oxygen	0.1382	0.00003186
Octane	3.788	0.0002374
Nitrous oxide	0.3832	0.00004415
Nitrogen trifluoride	0.358	0.0000545
Nitrogen dioxide	0.5354	0.00004424
Nitrogen	0.137	0.0000387
Nitric oxide	0.1358	0.00002789
Neopentane	1.717	0.0001411
Neon	0.02135	0.00001709
Methylamine	0.7106	0.0000588
Methanol	0.9649	0.00006702
Methane	0.2253	0.00004278
Mercury	0.82	0.00001696
Krypton	0.2349	0.00003978
Isobutane	1.332	0.0001164
Iodobenzene	3.352	0.0001656
Hydrogen sulfide	0.449	0.00004287
Hydrogen selenide	0.5338	0.00004637
Hydrogen iodide	0.6309	0.000053
Hydrogen fluoride	0.9565	0.0000739
Hydrogen cyanide	1.129	0.0000881
Hydrogen chloride	0.3716	0.00004081
Hydrogen bromide	0.451	0.00004431
Hydrogen	0.02476	0.00002661
Hydrazine	0.846	0.0000462
Hexane	2.471	0.0001735
Heptane	3.106	0.0002049
Helium	0.00346	0.0000238
Germanium tetrachloride	2.29	0.0001485
Furan	1.274	0.0000926
Freon	1.078	0.0000998
Fluoromethane	0.4692	0.00005264
Fluorobenzene	2.019	0.0001286
Fluorine	0.1171	0.000029
Ethylene	0.4612	0.0000582
Ethylamine	1.074	0.00008409
Ethyl acetate	2.072	0.0001412
Ethanol	1.218	0.00008407
Ethanethiol	1.139	0.00008098
Ethane	0.5562	0.0000638
Dodecane	6.938	0.0003758
Dimethyl sulfide	1.304	0.00009213
Dimethyl ether	0.818	0.00007246
Diethyl sulfide	1.9	0.0001214
Diethyl ether	1.761	0.0001344
Decane	5.274	0.0003043
Cyclopropane	0.834	0.0000747
Cyclohexane	2.311	0.0001424
Cyanogen	0.7769	0.00006901
Chloromethane	0.757	0.00006483
Chloroethane	1.105	0.00008651
Chlorobenzene	2.577	0.0001453
Chlorine	0.6579	0.00005622
Carbon tetrachloride	1.97483	0.0001281
Carbon monoxide	0.1505	0.00003985
Carbon disulfide	1.177	0.00007685
Carbon dioxide	0.364	0.00004267
Butane	1.466	0.0001226
Bromobenzene	2.894	0.0001539
Benzene	1.824	0.0001193
Argon	0.1355	0.00003201
Aniline	2.914	0.0001486
Ammonia	0.4225	0.0000371
Acetylene	0.4516	0.0000522
Acetonitrile	1.781	0.0001168
Acetone	1.602	0.0001124
Acetic anhydride	2.0158	0.0001263
Acetic acid	1.77098	0.0001065
2-Propanol	1.582	0.0001109
2-Butanone	1.997	0.0001326
1-Propanol	1.626	0.0001079
1-Pentanol	2.588	0.0001568
1-Octanol	4.471	0.0002442
1-Hexanol	3.179	0.0001856
1-Heptanol	3.817	0.000215
1-Dodecanol	7.57	0.000375
1-Decanol	5.951	0.0003086
1-Butanol	2.094	0.0001326
1-1-1-Trichloroethane	2.015	0.0001317

Pressure and Volume Calculation for Van der Waals Equation

The Van der Waals equation is an equation applies to the Real Gas Law but limited to temperature and pressure conditions, it includes two constants, a and b, to account for deviations from ideal behavior.

The calculator we have presented above makes the calculation for Pressure, Volume, Temperature and number of moles. Here we will clarify how the van der waals equation is rearranged to get the calculated value.

For Pressure calculation, the volume, temperature and the number of moles of the gas molecule are known, the pressure can be calculated using formula:

\[P=\frac{nRT}{V-nb} – \frac{n^2a} {V^2}\]

For Volume calculation of a real gas, V in term \(\frac{n^2a} {V^2}\) can be approximated as \(\frac{nR}{TP}\) as ideal gas. Therefore, V can be calculated as:

\[V= \frac{nR^3T^3}{PR^2T^2 + aP^2}+ nb\]

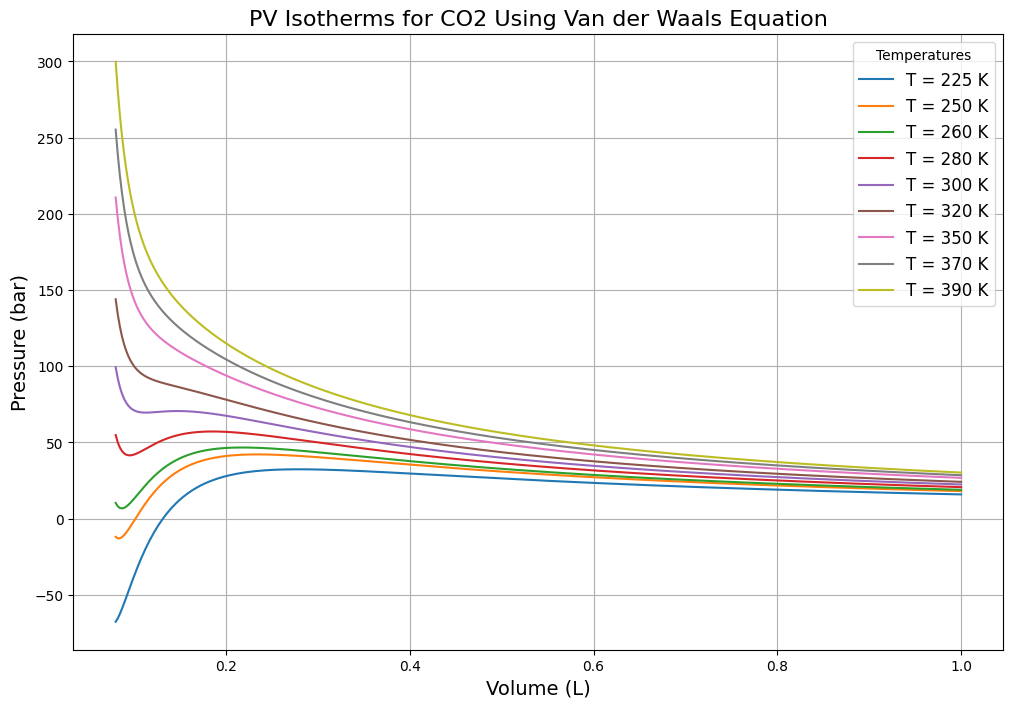
If we solve the cubic equation form of van der waals equation, it will lead to 3 roots, it can be further divided as 3 real roots or 1 real & 2 imaginary roots, which defines the plot on the PV isotherm.

Related: Hydraulic Diameter Calculator for Circular and Non-Circular cross-section

Related: Inverse Square Law for Radiation

Limitations of Van der Waals’ Equation

Van der Waals’ equation becomes invalid under actual condition as discussed below :

• The values of a and b (which are assumed to be constant) are found to vary with temperature. Thus the results obtained from the equation are incorrect when the variation of a and b is large with respect to temperature.
• The equation is not accurate enough in the critical region.

Example Problem on Van der Waals Equation

Carbon dioxide gas (1.00 mole) at 373 K occupies 536 mL at 50.0 atm pressure. What is the calculated value of the pressure using:

1. The Ideal Gas Equation
2. The Van der Waals Equation

Data given for Van der Waals constants for carbon dioxide: a = 3.61 L² atm mol^-2 & b = 0.0428 L/mol

Calculate the percentage deviation of each value from the observed pressure.

1. Using the Ideal Gas Equation

Given:

• V = 0.536 L
• n = 1.00 mol
• T = 373 K

The Ideal Gas Law is given by \(P = \frac{nRT}{V}\)

Solving for ( P ):
\(P = \frac{1.00 \times 0.0821 \times 373}{0.536}\)

\(P = 57.1 \, \text{atm}\)

The actual pressure is:
\(\text{Actual pressure} = 50.0 \, \text{atm}\)

The percentage deviation is calculated as:
% deviation \( = \left(\frac{7.1}{50.0}\right) \times 100 = 14.2 \%\)

2. Using the Van der Waals Equation

The Van der Waals equation is given by:

\(P=\frac{nRT}{V-nb} – \frac{n^2a} {V^2}\)

on substituting and solving the values we get, P = 49.6 atm

The percentage deviation is calculated as:
\( = \left(\frac{0.4}{50.0}\right) \times 100 = 0.8 \%\)

Therefore, using the Ideal Gas Law, the calculated pressure is 57.1 atm, resulting in a percentage deviation of 14.2% from the observed pressure of 50.0 atm. Using the Van der Waals equation, the calculated pressure is 49.6 atm, which has a percentage deviation of 0.8% from the observed pressure.

Also Read: Online Psychrometric Calculator for Chemical Engineers

Python Code for Van der Waals- PV Isotherm

This Python code helps user to calculate and visualizes the Pressure-Volume (PV) isotherms for carbon dioxide (CO₂) gas using the Van der Waals equation. Plots are generated at different temperatures which shows the relationship between pressure and volume changes with temperature.

Note: This Python code solves the specified problem. Users can copy the code and run it in a suitable Python environment. By adjusting the input parameters, users can observe how the output changes accordingly.

import numpy as np
import matplotlib.pyplot as plt

# Van der Waals constants for CO2
R = 0.08314  # L·bar·K⁻¹·mol⁻¹, gas constant
a = 3.640     # L²·bar·mol⁻²
b = 0.04267  # L·mol⁻¹

# Define the temperatures (in Kelvin) for the isotherms
temperatures = [225, 250, 260, 280, 300, 320, 350, 370, 390]  # temperatures

# Create an array of volume values
V = np.linspace(0.08, 1, 400)  # Volume in liters

# Create the plot
plt.figure(figsize=(12, 8))

for T in temperatures:
    # Van der Waals equation: P = [RT / (V - b)] - [a / (V^2)]
    P = (R * T) / (V - b) - (a / (V ** 2))
    
    # Plotting the isotherm
    plt.plot(V, P, label=f'T = {T} K')

# Plots
plt.xlabel('Volume (L)', fontsize=14)
plt.ylabel('Pressure (bar)', fontsize=14)
plt.title('PV Isotherms for CO2 Using Van der Waals Equation', fontsize=16)
plt.legend(title='Temperatures', fontsize=12)
plt.grid(True)

plt.show()

Output:

Resources

• Heat Transfer a Practical Approach – Book by Yunus A Çengel
• “Thermodynamics: An Engineering Approach” by Yunus A. Çengel and Michael A. Boles
• “Introduction to Chemical Engineering Thermodynamics” by J.M. Smith, H.C. Van Ness, and M.M. Abbott
• NPTEL Lectures on Thermodynamics
• Engineering Thermodynamics: A Textbook – by P.K Nag

Disclaimer: The Solver provided here is for educational purposes. While efforts ensure accuracy, results may not always reflect real-world scenarios. Verify results with other sources and consult professionals for critical applications. Contact us for any suggestions or corrections.