Table of Contents
Real gases show deviations from ideal gas behavior due to the assumptions for molecular interactions and finite molecular size, van der waals constants a and b are introduced in the Van der Waals equation of state to account for the deviations of real gases from ideal gas behavior.
The relationship between these constants and the critical properties – critical temperature (Tc), critical pressure (Pc), and critical volume (Vc) provides useful insights into the conditions under which gases can be liquefied and the nature of their phase transitions.
These critical constants are the conditions at which a substance can exist as both a liquid and a gas simultaneously. At these critical points, the properties of the gas and liquid phases become identical.
Related: Clausius Clapeyron Equation Calculator, Derivation and Applications
For the Van der Waals equation, the critical constants are related to the Van der Waals constants a and b as follows:
For Critical Temperature, \(T_c = \frac{8a}{27Rb} \)
For Critical Pressure, \(P_c = \frac{a}{27b^2} \)
For Critical Volume, \(V_c = 3b\)
Here, a represents the magnitude of the intermolecular attractive forces between gas molecules and b represents the effective volume occupied by gas molecules, often referred to as the excluded volume.
Click Here to download – Van der Waals constant data sheet for real gases
Van der Waals Equation
The Van der Waals Equation is first practical cubic equation of state which describes the behavior of real gases. It provides more accurate prediction about the behavior of real gases, especially under high pressure and low temperature conditions.
For one mole, the Van der Waals Equation of State is given by:
\[\left( P + \frac{a}{V_m^2} \right) (V_m – b) = RT\]
where:
- \( P \) is the pressure of the gas,
- \( V_m \) is the molar volume of the gas,
- \( T \) is the temperature,
- \( R \) is the universal gas constant,
- a & b are the van der waals constants.
Related: Kirchoff’s Law of Thermal Radiation, Wien’s Displacement Law
Related: Joule-Thomson Effect – Coefficient Calculation for CO2 and N2
Edition: 6th Edition, By: P.K. Nag
A comprehensive textbook on thermodynamics for engineering students, covering fundamental concepts and advanced applications with clear explanations and practical examples.
Buy on AmazonMeaning of Critical Constants
The critical constants – critical temperature (Tc), critical pressure (Pc), and critical volume (Vc) are specific properties of a substance that define the conditions at which it exhibits a unique phase behavior known as the critical point.
– Critical Temperature (Tc)
The critical temperature is the highest temperature at which a substance can exist as a liquid, above this temperature, a substance cannot be liquefied by pressure alone, and it exists only as a gas or supercritical fluid.
At Tc the properties of the gas and liquid phases become identical, leading to a single phase called a supercritical fluid, where distinct gas and liquid phases do not exist.
– Critical Pressure (Pc)
The critical pressure is the minimum pressure required to liquefy a gas at its critical temperature. At this pressure, the substance undergoes a phase transition from liquid to gas or vice versa without any distinct boundary between the phases.
Beyond the critical pressure, on applying additional pressure the substance cannot change a gas into a liquid unless the temperature is below critical temperature.
– Critical Volume (Vc)
The critical volume is the volume occupied by one mole of a substance at its critical temperature and critical pressure. It represents the specific volume at which the substance reaches to it critical points.
Also Read: Antoine Equation Calculator for Vapour Pressure versus Temperature Calculations
Also Read: Online Psychrometric Calculator for Chemical Engineers
Derivation for relation between Van der Waals Constants and Critical Constants
Continuing from the the Van der Waals equation of state for 1 mole (n=1) with molar volume \(V_m\), which is given as:
\[\left(P + \frac{a}{V_m^2}\right)(V_m – b) = RT\]
At the critical point, the first and second derivatives of pressure with respect to volume at constant temperature are zero:
The first derivative being zero \(\left(\frac{\partial P}{\partial V_m}\right)_{T_c} = 0\) the slope of the curve becomes horizontal, meaning there is no change in pressure with respect to volume at the critical temperature.
The second derivative being zero \(\left(\frac{\partial^2 P}{\partial V_m^2}\right)_{T_c} = 0\) means that this point is exactly an inflection point, where the nature of the curve (and thus the behavior of the substance) changes.
Now, rearranging the Van der Waals Equation in Terms of \(V_m\):
\[P = \frac{RT}{V_m – b} – \frac{a}{V_m^2}\]
On differentiating the above term with respect to \(V_m\), we get:
\[\frac{dP}{dV_m} = -\frac{RT}{(V_m – b)^2} + \frac{2a}{V_m^3}\]
At critical point, putting the derivative equal to zero at the critical point:
\[-\frac{RT_c}{(V_c – b)^2} + \frac{2a}{V_c^3} = 0\]
\[\frac{RT_c}{(V_c – b)^2} = \frac{2a}{V_c^3}\]
on rearrangement gives \(RT_c V_c^3 = 2a(V_c – b)^2\) ——————— eqn 1
taking second derivative with respect to (V_m) and putting it equal to zero:
\[\frac{d^2P}{dV_m^2} = \frac{2RT_c}{(V_m – b)^3} – \frac{6a}{V_m^4}\]
\[\frac{2RT_c}{(V_c – b)^3} – \frac{6a}{V_c^4} = 0\]
\[\frac{RT_c}{(V_c – b)^3} = \frac{3a}{V_c^4}\]
On rearrangement we get, \(RT_c V_c^4 = 3a(V_c – b)^3\) ———————— eqn 2
Divide the eqn2 by eqn 1 we get,
\[\frac{RT_c V_c^4}{RT_c V_c^3} = \frac{3a(V_c – b)^3}{2a(V_c – b)^2}\]
Simplifying above equation to find a relationship between Vc and b:
\[\frac{V_c}{V_c – b} = \frac{3}{2}\]
\[2V_c = 3(V_c – b)\]
\[V_c = 3b\]
Now, determining critical constants Tc and Pc with the help of Vc
Substitute \(V_c = 3b\) into the first derivative equation we get,
\[RT_c (3b)^3 = 2a(3b – b)^2\]
\[RT_c \cdot 27b^3 = 2a \cdot 4b^2\]
\[RT_c = \frac{8a}{27b}\]
\[T_c = \frac{8a}{27Rb}\]
Substituting Tc and Vc into the equation for pressure P
\[P_c = \frac{RT_c}{V_c – b} – \frac{a}{V_c^2}\]
\[P_c = \frac{R \left(\frac{8a}{27Rb}\right)}{3b – b} – \frac{a}{(3b)^2}\]
\[P_c = \frac{\frac{8a}{27b}}{2b} – \frac{a}{9b^2}\]
\[P_c = \frac{8a}{54b^2} – \frac{a}{9b^2}\]
\[P_c = \frac{8a}{54b^2} – \frac{6a}{54b^2}\]
\[P_c = \frac{a}{27b^2}\]
The relationships between the Van der Waals constants (a and b) and the critical constants (Tc, Pc, and Vc) are crucial for understanding and predicting the behavior of real gases under various conditions.

Physical Significance of Van der Waals Constants
The van der Waals constants a and b are having physical significance in describing the behavior of real gases:
- The constant a accounts for the attractive forces between gas molecules. It corrects the pressure in the van der Waals equation by considering these intermolecular attractions, which are not present in an ideal gas. A higher value of (a) indicates stronger intermolecular forces.
- The constant b represents the volume occupied by the gas molecules themselves. It corrects the volume in the van der Waals equation by accounting for the finite size of gas molecules, which is ignored in the ideal gas law. A larger value of (b) indicates larger gas molecules.
Also Read Hydraulic Diameter Calculator for Circular and Non-Circular cross-section
Also Read: Inverse Square Law for Radiation
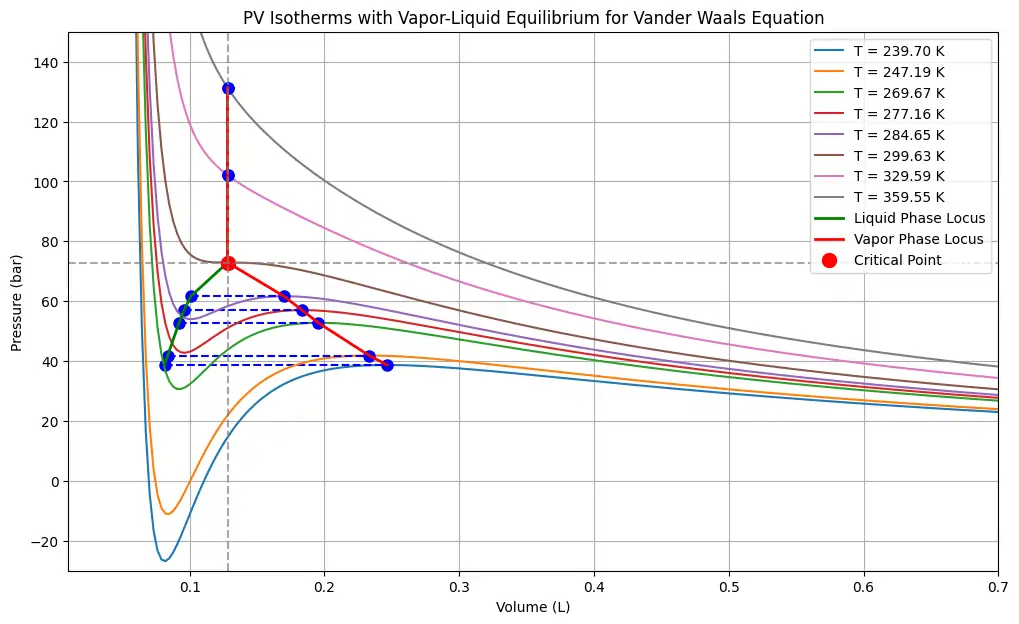
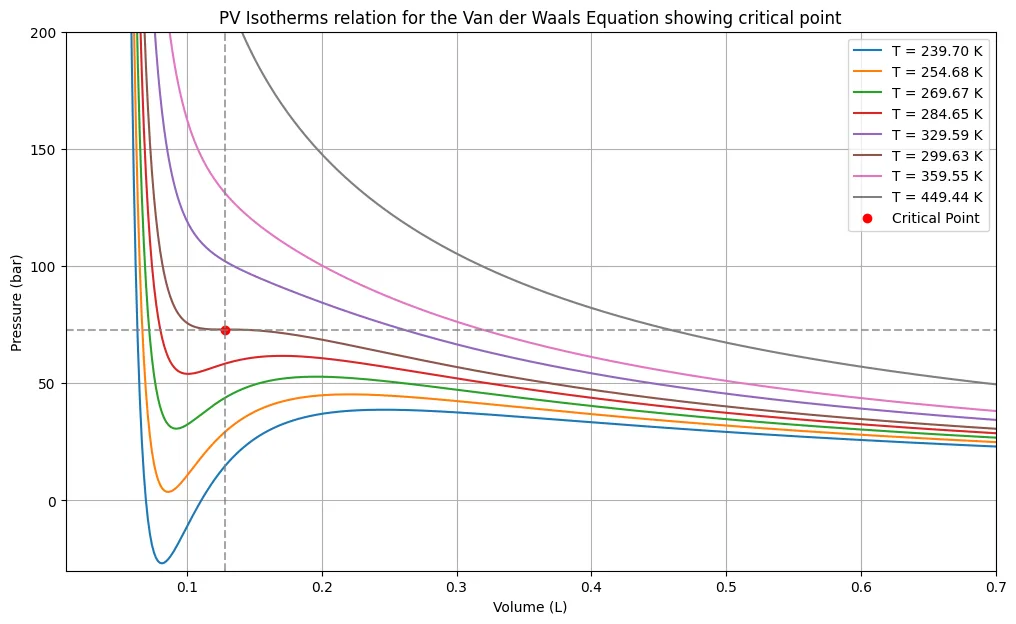
Python Code to plot PV isotherm for Van der Waals Equation
This Python code helps user to generate pressure-volume (PV) isotherms for a gas using the Van der Waals equation. It calculates the critical temperature, pressure, and volume for the gas, then plots the PV relationship at various temperatures, including below and above the critical temperature.
Note: This Python code solves the specified problem. Users can copy the code and run it in a suitable Python environment. By adjusting the input parameters, users can observe how the output changes accordingly.
import numpy as np
import matplotlib.pyplot as plt
# Van der Waals constants for a particular gas (e.g., CO2)
a = 3.59 # L^2 bar / mol^2
b = 0.0427 # L / mol
R = 0.08314 # L bar / (K mol)
# Calculate critical values
T_critical = (8 * a) / (27 * R * b)
P_critical = (a) / (27 * b**2)
V_critical = 3 * b
# Function to calculate P using Van der Waals equation
def van_der_waals_pressure(V, T):
return (R * T) / (V - b) - (a / V**2)
# Generate volumes and isotherms
V = np.linspace(0.05, 0.8, 500) # Volume range (L)
temperatures = [0.8 * T_critical, 0.85 * T_critical, 0.9 * T_critical, 0.95 * T_critical, 1.1 * T_critical, T_critical, 1.2 * T_critical, 1.5 * T_critical] # Additional temperatures
plt.figure(figsize=(10, 7))
for T in temperatures:
P = van_der_waals_pressure(V, T)
label = f'T = {T:.2f} K'
plt.plot(V, P, label=label)
# Marking the critical point
plt.plot(V_critical, P_critical, 'ro', label='Critical Point')
plt.axvline(V_critical, linestyle='--', color='gray', alpha=0.7)
plt.axhline(P_critical, linestyle='--', color='gray', alpha=0.7)
# Plot settings
plt.title('PV Isotherms relation for the Van der Waals Equation showing critical point')
plt.xlabel('Volume (L)')
plt.ylabel('Pressure (bar)')
plt.ylim(-30, 200)
plt.xlim(0.01, 0.7)
plt.legend()
plt.grid(True)
plt.show()Output:
Resources
- Heat Transfer a Practical Approach – Book by Yunus A Çengel
- “Thermodynamics: An Engineering Approach” by Yunus A. Çengel and Michael A. Boles
- “Introduction to Chemical Engineering Thermodynamics” by J.M. Smith, H.C. Van Ness, and M.M. Abbott
- NPTEL Lectures on Thermodynamics
- Engineering Thermodynamics: A Textbook – by P.K Nag
Disclaimer: The content provided here is for educational purposes. While efforts ensure accuracy, results may not always reflect real-world scenarios. Verify results with other sources and consult professionals for critical applications. Contact us for any suggestions or corrections.