Table of Contents
To understand the behaviour of thermal radiation in engineering, Kirchoff’s law of thermal radiation and Wien’s displacement law are the two fundamental principles that describe the emission and absorption of radiation by materials.
For example, you must have seen the colour variations in flames such as burning matchstick or kitchen stove, this is because of different objects emit radiation at various wavelengths depending on their temperatures. Therefore, to understand the behind why they appear different to our eyes it’s essential to explore some fundamental laws of radiation.
Related: Other heat transfer calculators
Kirchoff’s law of Thermal Radiation
Kirchoff’s law of thermal radiation or heat radiation states that, for a material in thermal equilibrium, the emissivity (\(\epsilon\)) of the material at a given wavelength (\(\lambda\)) and temperature (\(𝑇\)) is equal to its absorptivity (\(\alpha\)) at the same wavelength and temperature. This means that a good absorber of radiation at a particular wavelength is also a good emitter at that wavelength.
Mathematically, expressed as:
\[ \epsilon(\lambda, T) = \alpha(\lambda, T) \]
This equation signifies that at a given wavelength and temperature, the emissivity of a material equals its absorptivity.
At given wavelength and temperature the ratio of emissive power to the absorptive power of all bodies remain same. This ratio is equal to the emissive power of a perfect black body for the same temperature and wavelength.
Mathematical formula for Kirchoff’s law is given as:
\[\frac{\epsilon}{\alpha} = E_{\lambda}\]
where \(E_{\lambda}\) is the emissivity of black body.
Related: Thermal Radiation – Stefan Boltzmann Law Calculator
Terminologies Used in Kirchoff’s Law
Emissivity or Emissive Power (\(\epsilon\)):
A measure of a material’s ability to emit energy as thermal radiation compared to a perfect blackbody. It ranges from 0 to 1, where 1 indicates a perfect emitter.
\[\epsilon = \frac{\text{Radiant emittance of the material}}{\text{Radiant emittance of a blackbody}}\]
Absorptivity or Absorptive Power (\(\alpha\))
A measure of a material’s ability to absorb incident radiation. Like emissivity, it ranges from 0 to 1, where 1 indicates a perfect absorber.
\[\alpha = \frac{\text{Radiant flux absorbed by the material}}{\text{Incident radiant flux}}\]
Black Body Radiation :
A black body is an object that absorbs all radiation incident upon it, without reflecting or transmitting any. Due to its complete absorption and idealized nature, a blackbody also emits radiation across a wide range of wavelengths. Such electromagnetic radiation emitted by the black body are known as black body radiation.
Thermal Equilibrium
A state in which a system’s temperature is uniform and constant, with no net flow of energy in or out of the system i.e \(\frac{dQ}{dt} = 0\).
Wien’s Displacement Law
Wien’s Displacement Law was formulated by Wilhelm Wien in 1893. This law describes the relationship between the temperature of a blackbody radiator and the wavelength at which it emits the most radiation.
Mathematically, this law can be expressed as
\[\lambda_{\text{max}} \cdot T = \text{constant}\]
where,
- \(\lambda_{\text{max}}\) is the wavelength at which the radiation intensity is maximum,
- \(T\) is the temperature of the blackbody in Kelvin.
Wien’s Displacement Law implies that as the temperature of a blackbody increases, the wavelength at which it emits the most radiation decreases. In simpler terms, hotter objects emit shorter wavelength (higher frequency) radiation.
For example, the Sun, with its high temperature, emits most of its radiation in the visible spectrum, which is why we perceive it as bright and luminous.
Related: Thermal Radiation – Stefan Boltzmann Law Calculator
Related: Other heat transfer calculators
Theoretical Proof of Kirchoff’s law of Thermal Radiation
Kirchhoff’s law of thermal radiation can be theoretically derived by considering two bodies, A and B, suspended in an enclosure with a constant temperature. Body A is a regular material body while body B is a perfectly black body. According to heat exchange theory, all bodies emit and absorb thermal radiation.
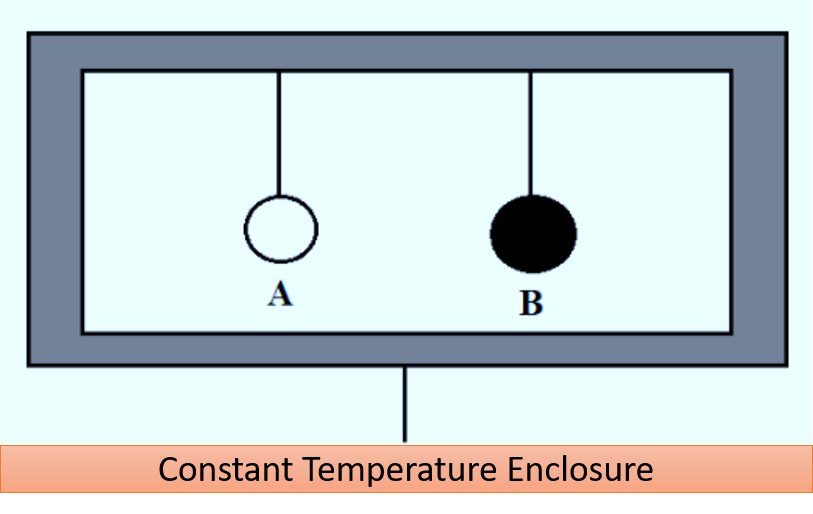
Let’s denote \(E\) as the emissive power of body A and \(\alpha\) its coefficient of absorption. Similarly, let \(E_B\) be the emissive power of body B. We denote \(Q\) as the radiant heat incident per unit time area of each body.
- Heat Exchange for Body A:
- Heat absorbed by body A per unit time per unit area: \(\alpha\)Q
- Heat emitted by body A per unit time per unit area: \(E\)
- Since the temperature remains constant, the heat absorbed equals the heat emitted: \(E=\alpha \cdot Q\)
- Heat Exchange for Body 𝐵:
- A perfectly black body absorbs all incident heat: Heat absorbed by body B per unit time per unit area: Q
- Heat emitted by body B per unit time per unit area: \(E_B\)
- Similarly, at constant temperature: \(E_B = Q\)
From the above equations, we have:
\( E = \alpha Q, \quad E_b = Q \)
Now, we know that the coefficient of emission, denoted by \(\epsilon \), is defined as the ratio of the emissive power of a body to that of a perfectly black body at the same temperature:
\( \epsilon = \frac{E}{E_b} \)
Substituting the values of \( E \) and \( E_b \) from the previous equations, we get:
\(\epsilon = \frac{\alpha Q}{Q} = \alpha \)
Since the coefficient of emission is the same as the coefficient of absorption, we conclude: \( \alpha = \epsilon \)
Thus, Kirchhoff’s law of thermal radiation is theoretically proven: the coefficient of emission is equal to the coefficient of absorption.
Related: Heat Transfer through Conduction Calculator
Related: Heat Transfer through Convection Calculator – Newton’s Law of Cooling
Practice Problems on Wien’s Displacement Law
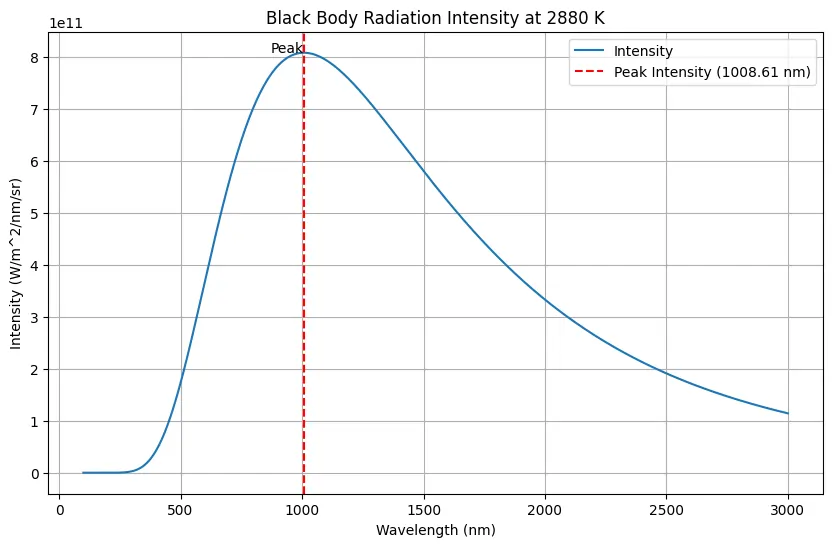
A black body is at a temperature of \(2880 \, \text{K}\). The energy of radiation emitted by this body with wavelength between \(499 \, \text{nm}\) and \(500 \, \text{nm}\) is \(U_1\), between \(999 \, \text{nm}\) and \(1000 \, \text{nm}\) is \(U_2\), and between \(1499 \, \text{nm}\) and \(1500 \, \text{nm}\) is \(U_3\). Wien’s constant, \(b = 2.88 \times 10^6 \, \text{nm} \cdot \text{K}\).
\(\lambda_m T = b \) (where b is Wien’s constant)
Wien’s displacement law states:
\( \lambda_m = \frac{b}{T}\)
\( = \frac{2.88 \times 10^6 \, \text{nm} \cdot \text{K}}{2880 \, \text{K}} = 1000 \, \text{nm} \)
The energy distribution with wavelength will be as follows:
From the graph it is clear that \(U_2 > U_1\) (in fact \(U_2\) is maximum).
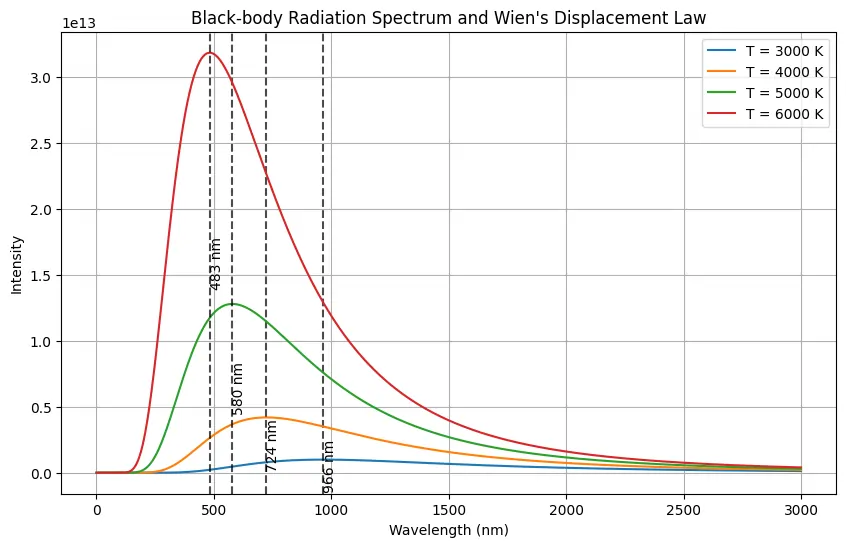
Python code for Wien’s Displacement Law and Black Body Radiation
This python code calculates and helps user to visualize the black-body radiation spectra for different temperatures using Planck’s law. It show Wien’s displacement law by plotting the intensity of radiation as a function of wavelength for temperatures of 3000 K, 4000 K, 5000 K, and 6000 K. For each temperature, it identifies and highlights the peak wavelength, showing how this peak shifts to shorter wavelengths as temperature increases. This shift illustrates the inverse relationship between the peak wavelength and temperature.
Note: This Python code solves the specified problem. Users can copy the code and run it in a suitable Python environment. By adjusting the input parameters, users can observe how the output changes accordingly.
import numpy as np
import matplotlib.pyplot as plt
from scipy.constants import h, c, k
def planck_law(wavelength, temperature):
"""Calculate black-body radiation intensity using Planck's law."""
return (2 * h * c**2) / (wavelength**5) * (1 / (np.exp((h * c) / (wavelength * k * temperature)) - 1))
def peak_wavelength(temperature):
"""Calculate the peak wavelength using Wien's displacement law."""
b_wavelength = 2.897771955e-3 # Wien's displacement constant in m*K
return b_wavelength / temperature
# Define a range of wavelengths (in meters)
wavelengths = np.linspace(1e-9, 3e-6, 1000) # from 1 nm to 3000 nm
# Define a range of temperatures (in Kelvin)
temperatures = [3000, 4000, 5000, 6000] # Example temperatures
# Plotting
plt.figure(figsize=(10, 6))
for T in temperatures:
intensity = planck_law(wavelengths, T)
plt.plot(wavelengths * 1e9, intensity, label=f'T = {T} K') # Convert wavelengths to nm for plotting
peak_wl = peak_wavelength(T) * 1e9 # Convert peak wavelength to nm
plt.axvline(peak_wl, color='k', linestyle='--', alpha=0.7)
plt.text(peak_wl, max(intensity) / 2, f'{peak_wl:.0f} nm', rotation=90, verticalalignment='center')
plt.xlabel('Wavelength (nm)')
plt.ylabel('Intensity')
plt.title('Black-body Radiation Spectrum and Wien\'s Displacement Law')
plt.legend()
plt.grid(True)
plt.show()Output:
Resources
- “Radiative Heat Transfer” by Michael F. Modest
- “Principles of Heat Transfer” by Frank Kreith and Raj M. Manglik
- “Introduction to Heat Transfer” by Theodore L. Bergman, Adrienne S. Lavine, Frank P. Incropera, and David P. DeWitt
- “Python Documentation” – Official guides and references for Python.
Disclaimer: The Solver provided here is for educational purposes. While efforts ensure accuracy, results may not always reflect real-world scenarios. Verify results with other sources and consult professionals for critical applications. Contact us for any suggestions or corrections.






