Inverse Square Law Calculator for Radiation and python code solution

The Inverse Square Law is a fundamental principle in physics that describes how the intensity of a physical quantity, such as radiation, changes with distance from its source.

Inverse Square Law states that the intensity of radiation is inversely proportional to the square of the distance from the radiation source.

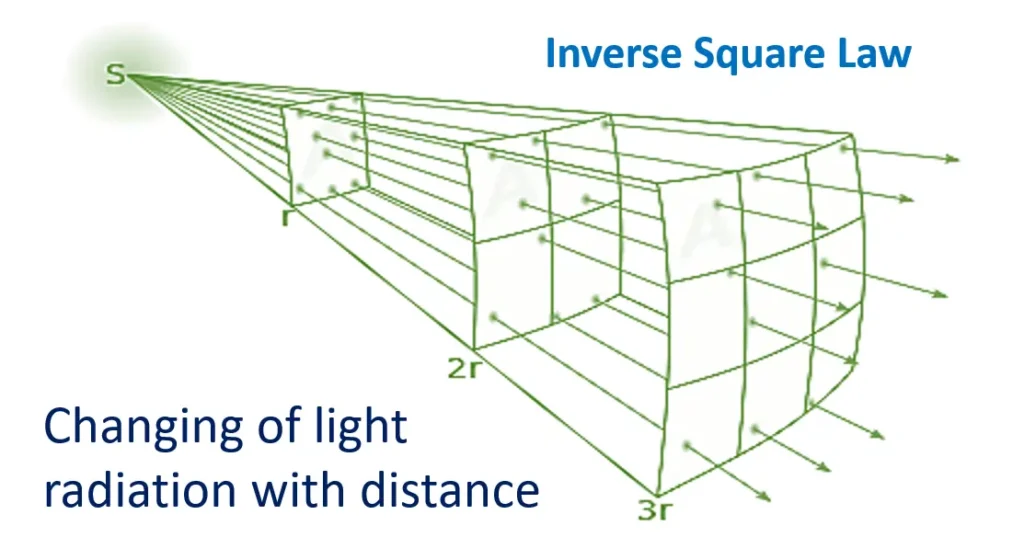
In simple words, as you move farther away from a source of radiation, the intensity of the radiation decreases rapidly. This law is applicable to various forms of radiation, including light, sound, and electromagnetic waves.

Mathematically, it can be expressed as:

\[ \text{intensity} \propto \frac{1}{\text{distance}^2} \]

where, \( I \) is the intensity varying as a function of distance (\( d \)) from some center

\[ \frac{{\text{intensity}_1}}{{\text{intensity}_2}} = \frac{{\text{distance}_2^2}}{{\text{distance}_1^2}} \]

Or as the formulation of a constant quantity:

\[\text{I}_1 \times \text{d}_1^2 = \text{I}_2 \times \text{d}_2^2 \]

Related: Thermal Radiation – Stefan Boltzmann Law Calculator

Related: Hydraulic Diameter Calculator for Circular and Non-Circular cross-section

Inverse Square Law Calculator

This calculator computes the initial or final intensity of radiation and the initial or final distance based on the inverse square law principle.

Note: This calculator is designed to solve for one unknown variable at a time using the inverse square law principle. Please ensure that only one variable is designated as ‘x’ while entering values.

Related:  Heat Transfer through Conduction Calculator

Related: Heat Transfer through Convection Calculator – Newton’s Law of Cooling

Example Problem on Inverse Square Law

The intensity of a sound wave is 6 × 10^–3  W/m² at a distance of 4m from the source. What is the intensity of the sound at a distance of 10m from the source?

Given:

• Initial Intensity of Radiation (\(I_1\)) = \(6 \times 10^{-3}\) W/m²
• Initial Intensity of Radiation (\(I_2\)) = x W/m²
• Distance 1 (\(d_1\)) = 4 m
• Distance 2 (\(d_2\)) = 10 m

using inverse square law for radiation,

\(\text{I}_1 \times \text{d}_1^2 = \text{I}_2 \times \text{d}_2^2 \)

\(I_2\) = (6 x 10^-3) x (4²) / (10²)

\(I_2\) = (6 x 10^-3) x (16) / (100)

\(I_2\) = \(9.6 \times 10^{-4}\) W/m²

Therefore, the intensity of light radiation at a distance of 10 m from a distance of 4 m to be \(9.6 \times 10^{-4}\) W/m²

Related: Joule-Thomson Effect – Coefficient Calculation for CO2 and N2

Python Code for Inverse Square Law

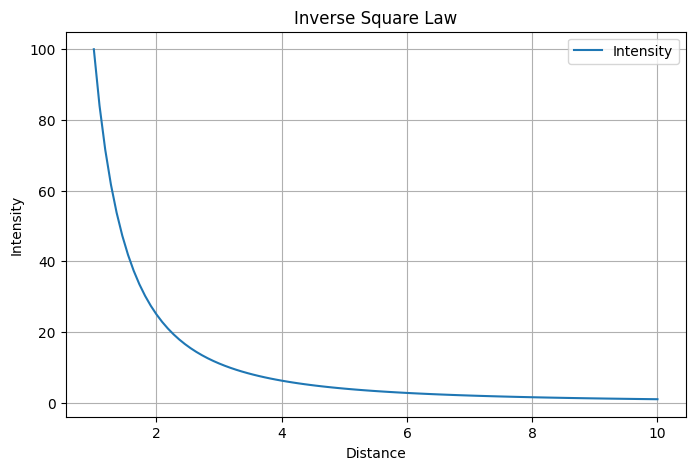
This python code helps user to calculate intensity using the inverse square law formula. It then generates a range of distances, calculates intensities based on the given reference intensity, and plots the relationship between distance and intensity on a graph with distance on the x-axis and intensity on the y-axis.

Note: This Python code solves the specified problem. Users can copy the code and run it in a suitable Python environment. By adjusting the input parameters, users can observe how the output changes accordingly.

import numpy as np
import matplotlib.pyplot as plt

# Function to calculate inverse-square-law
def inverse_square_law(distance, intensity_at_reference_point):
    return intensity_at_reference_point / (distance ** 2)

# Generate distances
distances = np.linspace(1, 10, 100)

# Intensity at a reference point (you can adjust this value)
intensity_at_reference_point = 100 # user can change the values as desired

# Calculate intensities using inverse square law
intensities = inverse_square_law(distances, intensity_at_reference_point)

# Plot
plt.figure(figsize=(8, 6))
plt.plot(distances, intensities, label='Intensity')
plt.title('Inverse Square Law')
plt.xlabel('Distance')
plt.ylabel('Intensity')
plt.legend()
plt.grid(True)
plt.show()

Output:

Resources:

1. “Principles of Heat Transfer” by Frank Kreith and Raj M. Manglik
2. “Introduction to Heat Transfer” by Theodore L. Bergman, Adrienne S. Lavine, Frank P. Incropera, and David P. DeWitt
3. “Python Documentation” – Official guides and references for Python.
4. “Classical Mechanics” by John R. Taylor

Disclaimer: The Solver provided here is for educational purposes. While efforts ensure accuracy, results may not always reflect real-world scenarios. Verify results with other sources and consult professionals for critical applications. Contact us for any suggestions or corrections.