Table of Contents
To understand the behavior of gases and how it varies with pressure, temperature, volume, or the amount of gas, the ideal gas equation is used. It relates these state variables to help predict gas behavior.
Fundamental gas laws such as Boyle’s Law, Charles’s Law, Gay-Lussac’s Law, and Avogadro’s Law are used to study how gases react, move, or change under different conditions.
Here, we provide an all-in-one Gas Laws Calculator that can solve for the unknown parameter in an equation when the other variables are known.
Related: Specific Heat Capacity Calculation for Water and Other Substances
Related: Water Density & Specific Weight Calculation – Variation with temperature and Pressure
Gas Laws Calculator
This Gas Laws Calculator is used to perform calculations for gas laws, including Boyle’s Law, Charles’s Law, Gay-Lussac’s Law, Avogadro’s Law, and the Ideal Gas Equation.
User can calculate the unknown variables (pressure, volume, temperature, or moles) by inputting known values. It supports SI, MKS, and CGS unit systems, with temperature options in Kelvin, Celsius, or Fahrenheit.
Related: Van der Waals Equation Calculator and PV Isotherm for Real Gases
Related: Relation Between Van der Waals Constants and Critical Constants
How is Ideal Gas Equation Formed
The ideal gas equation, expressed as PV = nRT, was formulated by combining empirical laws developed by several scientists. Boyle’s Law, Charles’s Law, Avogadro’s Law, and Gay-Lussac’s Law were integrated to create this unified equation, which relates pressure (P), volume (V), number of moles (n), the universal gas constant (R), and temperature (T).
From Boyle’s Law: V ∝ 1/P (at constant T)
From Charles’s Law: V ∝ T (at constant P)
From Avogadro’s Law: V ∝ n (at constant T and P)
Combining these proportionalities, we get: V ∝ nT/P
To convert this proportionality into an equation, the universal gas constant, R is introduced. Therefore, the equation becomes V=nRT/P.
On rearranging, we get PV=nRT, which is a theoretical construct commonly known as the Ideal Gas Equation.
Also Read: Antoine Equation Calculator for Vapour Pressure versus Temperature Calculations
Also Read: Online Psychrometric Calculator for Chemical Engineers
Applicability of Ideal Gas Law
An ideal gas is a hypothetical gas whose particles are assumed to have no intermolecular forces, occupy no volume, and undergo perfectly elastic collisions. An ideal gas simplify the complex gas behavior.
The ideal gas law, PV=nRT, is valid under conditions where a gas approximates ideal behavior. It is most applicable in the following scenarios:
- Low Pressures: When the pressure is low (near or below 1 atm), gas molecules are far apart and they interact very little with each other. Under such conditions gases like N2, O2, He tend to behave almost like ideal gases.
- High Temperatures: At high temperatures – the molecules move rapidly, and their kinetic energy overcomes any attractive forces between them. This makes the gas behave more ideally.
- Dilute Gases: In systems where the gas is very dilute (low in density), the molecules are widely spaced. The assumptions of negligible volume and no interactions becomes valid.
- Non-Polar, Simple Gases: Monatomic (e.g., helium, argon) or diatomic gases (e.g., nitrogen, oxygen) with weak intermolecular forces closely follow the ideal gas law under standard conditions like 0°C and 1 atm pressure.
Related: Joule-Thomson Effect – Coefficient Calculation for CO2 and N2
Related: Hydraulic Diameter Calculator for Circular and Non-Circular cross-section
How is Ideal Gas different from Real Gas
Real gases are actual gases that exist in nature, such as O₂, N₂, NH₃, and water vapor (H₂O). These gases have molecules with finite volume and experience attractive and repulsive intermolecular forces.
These properties cause ideal gases to deviate from the real gases under certain conditions, particularly at high pressures and low temperatures.
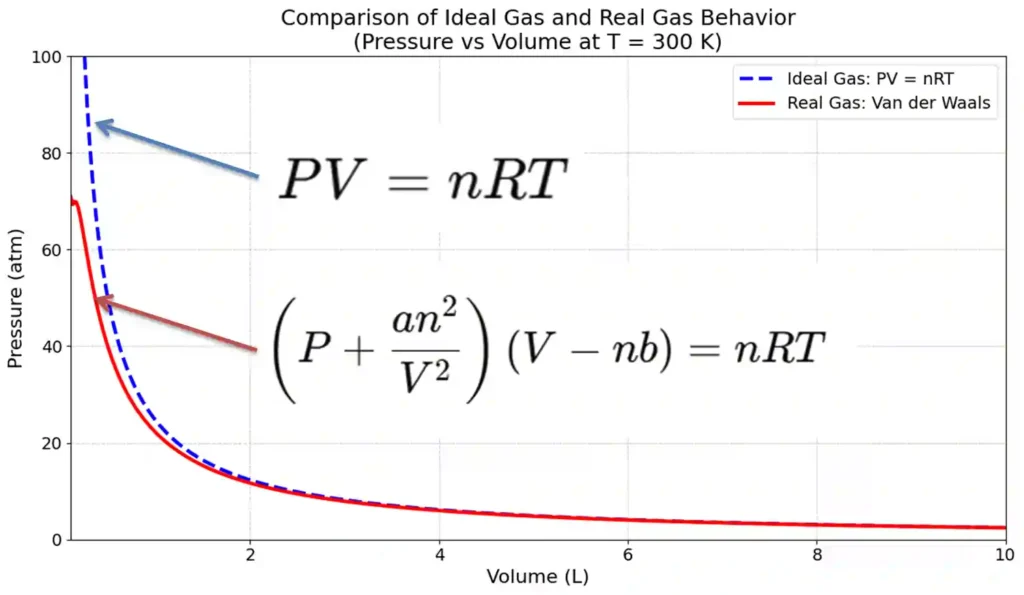
Below is a table provided to compare the ideal gases and real gases, showing the differences based on their properties, behavior, and the conditions under which they deviate.
| Ideal Gas | Real Gas |
|---|---|
| Theoretical gas with no intermolecular forces and negligible molecular volume. | Real gases with intermolecular forces and finite molecular volume. |
| Molecules interact with perfectly elastic collisions. | Attractive and repulsive forces (e.g., van der Waals, hydrogen bonding) present, especially at high pressures or low temperatures. |
| Molecules assumed to have zero volume (point particles). | Molecules have finite volume, significant at high pressures. |
| Obeys PV = nRT exactly under all conditions. | Approximates PV = nRT at low pressures and high temperatures; deviates at high pressures (>50 atm) or low temperatures (near liquefaction). |
| Hypothetical; no real gas is perfectly ideal. | O₂, N₂, CO₂, NH₃, He, H₂O vapor etc. |
| Ideal behavior assumed universally. | Real gas deviates at high pressures (molecular crowding) and low temperatures (strong attractive forces). |
Related: Hydraulic Diameter Calculator for Circular and Non-Circular cross-section
Also Read: Online Psychrometric Calculator for Chemical Engineers
Resources
- “Thermodynamics: An Engineering Approach” by Yunus A. Çengel and Michael A. Boles
- “Introduction to Chemical Engineering Thermodynamics” by J.M. Smith, H.C. Van Ness, and M.M. Abbott
- NPTEL Lectures on Thermodynamics
Disclaimer: The Solver provided here is for educational purposes. While efforts ensure accuracy, results may not always reflect real-world scenarios. Verify results with other sources and consult professionals for critical applications. Contact us for any suggestions or corrections




Good information fot revision for anyone interested