Hydraulic Diameter Calculator for Circular and Non-Circular cross-section

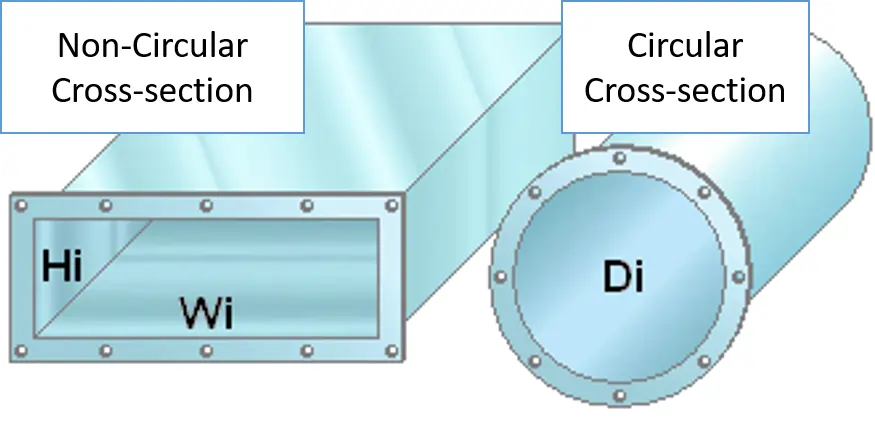
What is Hydraulic Diameter?

The hydraulic diameter is a parameter which is used for handling flow in non-circular tubes and channels. It’s not a physical diameter, but a calculated value that takes into account the shape of the flow channel.

The hydraulic diameter, \(D_H\), is defined as four times the cross-sectional area of the channel divided by the wetted perimeter.

\[D_H = \frac{4A}{P}\]

where:

• (A) is the cross-sectional area of the flow
• (P) is the wetted perimeter of the cross-section

Note: Wetted Perimeter includes all surfaces acted upon by shear stress from the fluid.

For a circular pipe, the hydraulic diameter is simply the diameter of the pipe. For non-circular cross-section channels, such as a rectangular duct, the \(D_H\) is calculated using the above formula.

Related: Newton’s Law of Viscosity Calculator – Dynamic Viscosity

Related: Other Fluid Mechanics Calculators

Hydraulic Diameter Calculator for Non-Circular Cross-section

This calculator computes the \(D_H\) of a channel or pipe. Users input the height of the duct in meters (h) and width of the duct in meters (W), and the calculator uses the formula \(D_h = \frac{4 \times WH}{2(W+H)}\). This value is useful in fluid dynamics calculations, particularly in determining flow characteristics in non-circular conduits flow situations.

Related: Hagen-Poiseuille Equation Calculator / Poiseuille’s Law Solver

Hydraulic Diameter Calculator for Circular Cross-section

This calculator computes the \(D_H\) of a channel or pipe given its cross-sectional area and wetted perimeter for a circular cross-section. Users input the area (A) in square meters and the wetted perimeter (P) in meters, and the calculator uses the formula \(D_h = \frac{4A}{P}\). This value is useful in fluid dynamics calculations, particularly in determining flow characteristics in circular conduits flow situations.

List of Hydraulic Diameters

Geometry	Hydraulic Diameter	Comment
Circular tube	\[ D_H = \frac{4 \cdot \frac{\pi D^2}{4}}{\pi D} = D \]	For a circular tube, the hydraulic diameter is equal to the diameter of the tube.
Annulus	\[ D_H = \frac{4 \cdot \frac{\pi (D_{\text{out}}^2 – D_{\text{in}}^2)}{4}}{\pi (D_{\text{out}} + D_{\text{in}})}\] \[ D_H = D_{\text{out}} – D_{\text{in}} \]	For an annulus, \(D_{in}\) \(D_{out}\) represents the inner and outer diameter of the annulus.
Square duct	\[ D_H = \frac{4a^2}{4a} = a \]	Here, \( a \) represents the length of a side
Rectangular duct (fully filled)	\[ D_H = \frac{4ab}{2(a+b)} \]​ \[D_H = \frac{2ab}{a+b} \]​	For special case of a very wide duct, i.e., a slot of width \( b \), where \( b \gg a \), then \( D_H = 2a \).
Partially filled rectangular duct (open from top)	\[ D_H = \frac{4ab}{2a + b} \]	For special case of a very wide duct, i.e., a slot of width \( b \), where \( b \gg a \), and \( a \) is the water depth, then \( D_H = 4a \).​

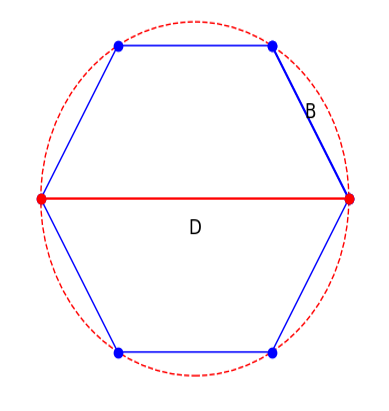
Hydraulic Diameter for Regular Polygon

For a fully filled duct or pipe whose cross-section is a regular polygon, the \(D_H\) is equivalent to the diameter \( D \) of a circle inscribed within the wetted perimeter.

Python Code for Hydraulic Diameter

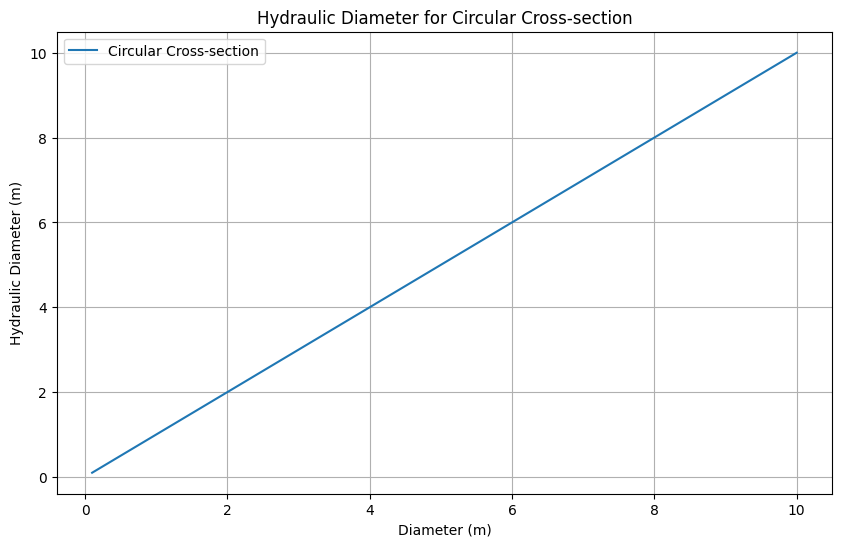
This Python code helps user to calculate hydraulic diameter for different cross-sections, specifically circular and rectangular. For circular cross-sections, the code calculates the \(D_h\) for different diameters. For rectangular cross-sections, it calculates the hydraulic diameter for different widths and heights.

Note: This Python code solves the specified problem. Users can copy the code and run it in a suitable Python environment. By adjusting the input parameters, users can observe how the output changes accordingly.

import numpy as np
import matplotlib.pyplot as plt

# Function to calculate hydraulic_diameter
def hydraulic_diameter(area, perimeter):
    return 4 * area / perimeter

# Circular cross-section
diameter = np.linspace(0.1, 10, 100)  # Diameter in meters
circular_area = np.pi * (diameter / 2)**2
circular_perimeter = np.pi * diameter
circular_dh = hydraulic_diameter(circular_area, circular_perimeter)

# Plotting for circular cross-section
plt.figure(figsize=(10, 6))
plt.plot(diameter, circular_dh, label='Circular Cross-section')
plt.xlabel('Diameter (m)')
plt.ylabel('Hydraulic Diameter (m)')
plt.title('Hydraulic_Diameter for Circular Cross-section')
plt.legend()
plt.grid(True)
plt.show()

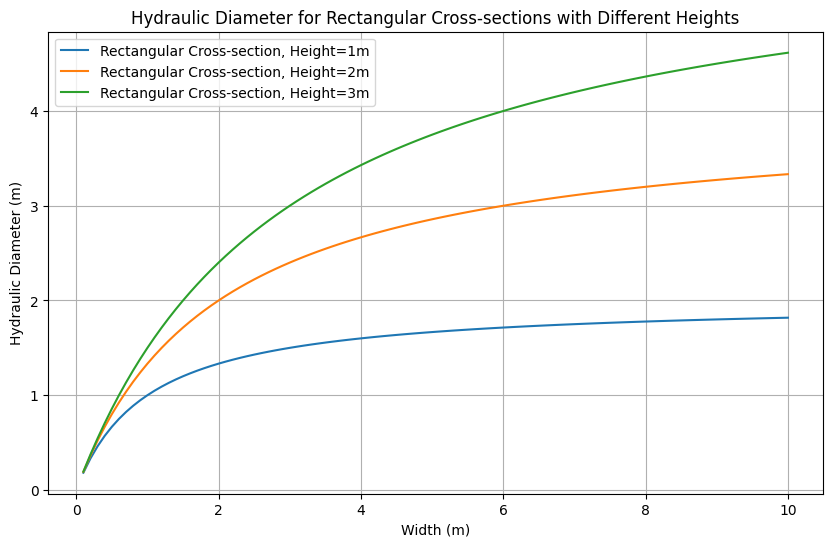
# Rectangular cross-section for different heights
width = np.linspace(0.1, 10, 100)  # Width in meters
heights = [1, 2, 3]  # Different heights in meters

plt.figure(figsize=(10, 6))
for height in heights:
    rectangular_area = width * height
    rectangular_perimeter = 2 * (width + height)
    rectangular_dh = hydraulic_diameter(rectangular_area, rectangular_perimeter)
    plt.plot(width, rectangular_dh, label=f'Rectangular Cross-section, Height={height}m')

plt.xlabel('Width (m)')
plt.ylabel('Hydraulic_Diameter (m)')
plt.title('Hydraulic_Diameter for Rectangular Cross-sections with Different Heights')
plt.legend()
plt.grid(True)
plt.show()

Output:

Resources

1. “Fluid Mechanics” by Frank M. White
2. “Introduction to Fluid Mechanics” by Robert W. Fox, Alan T. McDonald, and Philip J. Pritchard
3. “Principles of Heat and Mass Transfer” by Frank P. Incropera and David P. DeWitt
4. Python.org – The official Python website offers tutorials, documentation, and resources for learning Python.

Disclaimer: The Solver provided here is for educational purposes. While efforts ensure accuracy, results may not always reflect real-world scenarios. Verify results with other sources and consult professionals for critical applications. Contact us for any suggestions or corrections.