Table of Contents
In chemical engineering, both heat and mass transfer are essential processes governing the movement of thermal energy and matter in various systems. Heat and mass transfer analogy between these two transfer phenomena allows engineers to analyze and solve problems more efficiently by using similar approaches.
These analogies simplifies the analysis of systems like reactors, distillation columns and heat exchangers where both heat and mass transfer occurs.
Related: 10 Mostly used Dimensionless Numbers in Chemical Engineering
Heat and Mass Transfer Basics
In both heat and mass transfer processes transport occurs due to gradients. Temperature gradient for heat and Concentration gradient for mass—to drive the transfer.
In Heat Transfer the movement of thermal energy due to a temperature difference. It can occur through conduction, convection, or radiation. Fourier’s Law of Heat Conduction describes how heat flows from regions of higher temperature to lower temperature. The heat flux is proportional to the negative temperature gradient:
\[q = -k \frac{dT}{dx}\]
Related: Heat Transfer through Convection Calculator – Newton’s Law of Cooling
In Mass Transfer the movement of a substance from one location to another due to a concentration gradient. This usually occurs through diffusion or convection. Fick’s Law of Diffusion is analogous to Fourier’s law and describes how mass flows due to a concentration difference. The mass flux is proportional to the negative concentration gradient:
\[J = -D \frac{dC}{dx}\]
Related: Fick’s second law of Diffusion
Here is the table below, which provides the analogy and comparison between heat and mass transfer.

Related: Kirchoff’s Law of Thermal Radiation, Wien’s Displacement Law
Related: Joule-Thomson Effect – Coefficient Calculation for CO2 and N2
Dimensionless Numbers Analogy in Heat and Mass Transfer
Heat and Mass transfer analogy can also be explained in terms of dimensionless numbers. It tells the similarity between both the processes and provides understanding how mathematical principles are applied to both the phenomenon.
Related: Nusselt Number Calculator – Significance and Calculation
Here we have provided the summarized table for the dimensionless number analogy in heat and mass transfer.
| Aspect | Heat Transfer | Mass Transfer |
|---|---|---|
| Nusselt Number (Nu) & Sherwood Number (Sh) | Formula: \(\text{Nu} = \frac{hL}{k}\) Nu compares convective to conductive heat transfer. A high Nu indicates convection dominates over conduction, typically used in designing heat exchangers. | Formula: \(\text{Sh} = \frac{k_m L}{D}\) Sh is the mass transfer analog of Nu. A high Sh shows effective convective mass transfer over diffusion. |
| Prandtl Number (Pr) & Schmidt Number (Sc) | Formula: \(\text{Pr} = \frac{\nu}{\alpha} = \frac{\mu C_p}{k}\) Pr relates the relative thickness of the velocity boundary layer to the thermal boundary layer. High Pr indicates slow heat transfer (e.g., oil), while low Pr shows rapid heat transfer (e.g., liquid metals). | Formula: \(\text{Sc} = \frac{\nu}{D}\) Sc is the mass transfer equivalent of Pr. It compares the relative thickness of the velocity boundary layer to the mass boundary layer. High Sc means slow mass diffusion (e.g., gases in liquids). |
| Reynolds Number (Re) | Formula: \(\text{Re} =\frac{\rho u L}{\mu}\) Re is useful in determining heat transfer regimes. Low Re (laminar) means smooth, orderly flow, while high Re (turbulent) means chaotic, mixing flow. | Formula: \(\text{Re} =\frac{\rho u L}{\mu}\) Re also determines the flow regime in mass transfer processes. Laminar flow promotes diffusion, while turbulent flow enhances convective mass transfer. |
| Grashof Number (Gr) | Formula: \(\text{Gr} = \frac{g \beta \Delta T L^3}{\nu^2}\) Gr describes the significance of buoyancy forces in free convection. High Gr leads to stronger convective currents due to natural heat transfer (e.g., heating a fluid in a tank). | Formula: \(\text{Gr} = \frac{g \beta \Delta C L^3}{\nu^2}\) Gr in mass transfer indicates the importance of buoyancy forces in natural convection mass transfer. Similar to heat transfer, but driven by concentration gradients. |
| Convective Regimes | Re indicates flow regime (laminar or turbulent), while Nu provides heat transfer behavior. | Like Nu, Sh depends on Re to determine the nature of convective mass transfer. |
Related: Thermal Boundary Layer Thickness (δT) for Flat Plate
Also Read: Arrhenius Activation Energy Calculator for two temperatures
Heat and Mass Transfer Correlations
Heat and mass transfer correlations are empirical and theoretical relationships that tells the rate at which energy or mass is transferred between phases in various engineering systems.
Edition: Revised 2nd Edition, By: R. Byron Bird, Warren E. Stewart, Edwin N. Lightfoot
Comprehensive coverage of transport phenomena, including momentum, heat, and mass transfer. Updated content for better clarity.
Buy on AmazonThese correlations helps in predicting transfer rates in practical scenarios like heat exchangers, reactors, and separation processes. Here we are providing the summarized table for the heat and mass transfer correlations and their usage in chemical engineering.
| Aspect | Heat Transfer Correlations | Mass Transfer Correlations | Usage |
|---|---|---|---|
| Dittus-Boelter Equation (Turbulent Flow) | \[\text{Nu} = 0.023 \, \text{Re}^{0.8}\] | \[\text{Sh} = 0.023 \, \text{Re}^{0.8}\] | Used for calculating convective heat/mass transfer in turbulent flow in pipes. |
| Sieder-Tate Equation (Viscous Fluids) | \[\text{Nu} = 0.027 \, \text{Re}^{0.8} \, \text{Pr}^{1/3} \, \left(\frac{\mu}{\mu_w}\right)^{0.14}\] | \[\text{Sh} = 0.027 \, \text{Re}^{0.8} \, \text{Sc}^{1/3} \, \left(\frac{\mu}{\mu_w}\right)^{0.14}\] | Applied in heat/mass transfer for viscous fluids with changing viscosity along the boundary layer. |
| Colburn Equation (Heat Transfer) | \[\text{Nu} = 0.023 \, \text{Re}^{0.8} \, \text{Pr}^{0.4}\] | \[\text{Sh} = 0.023 \, \text{Re}^{0.8} \, \text{Sc}^{0.4}\] | Colburn j-factor is used for combined heat and mass transfer in turbulent flows. |
| Chilton-Colburn Analogy | \[\frac{\text{Nu}}{\text{Re}^{0.8}} = j_H = j_D \] | \[\frac{\text{Sh}}{\text{Re}^{0.8}} = j_D\] | Useful for relating heat and mass transfer rates in systems with similar flow conditions. |
| Natural Convection (Vertical Plate) | \[\text{Nu} = 0.59 \, \text{Gr}^{1/4} \, \text{Pr}^{1/4}\] (laminar) | \[\text{Sh} = 0.59 \, \text{Gr}^{1/4} \, \text{Sc}^{1/4}\] (laminar) | For calculating heat and mass transfer in natural convection near vertical surfaces. |
| Forced Convection over Flat Plate | \[\text{Nu} = 0.332 \, \text{Re}^{1/2} \, \text{Pr}^{1/3}\] (laminar) | \[\text{Sh} = 0.332 \, \text{Re}^{1/2} \, \text{Sc}^{1/3}\] (laminar) | Applied in systems where flow occurs over a flat plate, such as heat exchangers. |
| Heat Transfer in Packed Beds | \[\text{Nu} = 2 + 1.1 \, \text{Re}^{1/2} \, \text{Pr}^{1/3}\] | \[\text{Sh} = 2 + 1.1 \, \text{Re}^{1/2} \, \text{Sc}^{1/3}\] | Used in catalytic reactors and adsorption columns for heat and mass transfer. |
Also Read:: Clausius Clapeyron Equation Calculator, Derivation and Applications
Also Read: Interactive McCabe-Thiele Diagram Calculator for Binary Distillation
Heat and Mass Transfer Analogies
The analogy between heat and mass transfer is based on the similarity of the governing equations for both processes. These analogy allows to predict one type of transfer coefficient (e.g., mass transfer) using the known value of another (e.g., heat transfer). Here are some common analogies:
– Reynolds Analogy (Pr ≈ Sc ≈ 1)
The Reynolds analogy relates the momentum transfer (friction factor) to heat and mass transfer. The Reynolds analogy relates the convective heat transfer coefficient and the mass transfer coefficient and it is expressed as:
\[\frac{h}{\rho C_p u} = \frac{k_m}{u}\]
where, h is the heat transfer coefficient, ρ is the fluid density, Cp is the specific heat, u is the velocity, and km is the mass transfer coefficient.
Note: This analogy is most accurate for systems where the Prandtl and Schmidt numbers are equal.
This relationship can also be expressed in terms of dimensionless numbers as:
\[\frac{\text{Nu}}{\text{Re} \cdot \text{Pr}} = \frac{\text{Sh}}{\text{Re} \cdot \text{Sc}} = \frac{f}{2}\]
where:
- Nu is the Nusselt number
- Re is the Reynolds number
- Pr is the Prandtl number
- Sh is the Sherwood number
- Sc is the Schmidt number
- f is the friction factor
– Chilton-Colburn Analogy (Pr ≠ Sc ≠ 1)
This analogy is the extension of Reynolds analogy and is widely used for systems where Pr and Sc may differ significantly. it is expressed using the Colburn j-factors for heat and mass transfer:
\[j_H = \frac{\text{Nu}}{\text{Re}^{0.8} \cdot \text{Pr}^{1/3}} =j_D\]
\[j_D = \frac{\text{Sh}}{\text{Re}^{0.8} \cdot \text{Sc}^{1/3}} = j_H\]
Note: Applicable to both laminar and turbulent flows, but primarily for turbulent boundary layers.
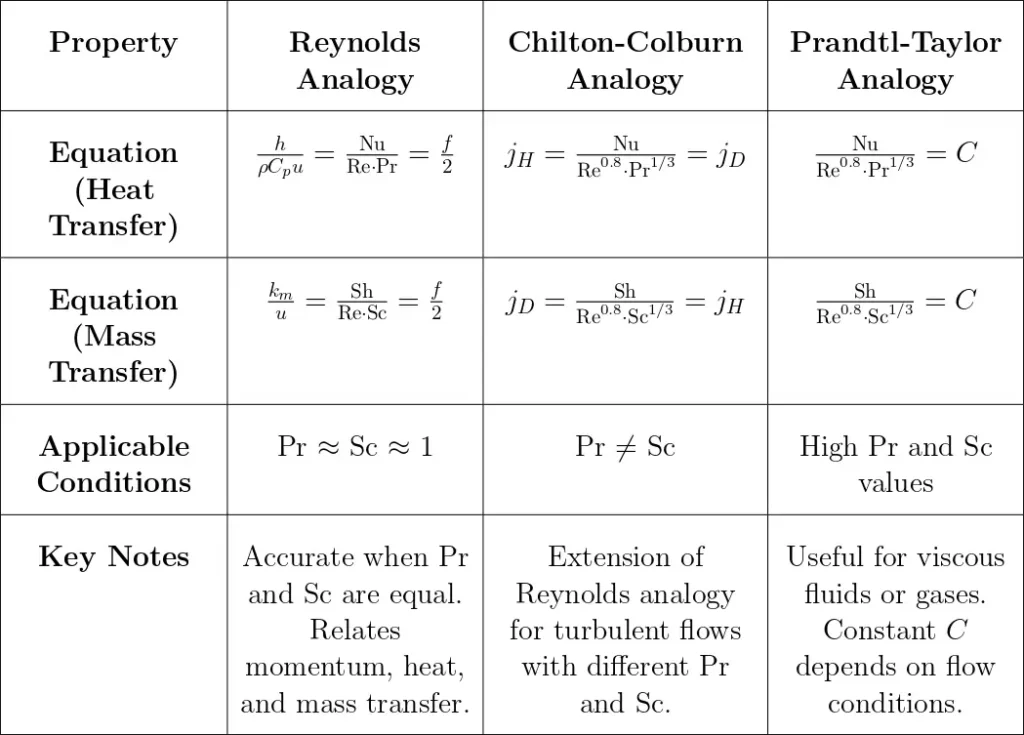
– Prandtl-Taylor Analogy
The Prandtl-Taylor analogy relates the Nusselt number (Nu) for heat transfer and the Sherwood number (Sh) for mass transfer to the Reynolds number (Re) and the Prandtl or Schmidt numbers. The analogy is expressed as:
\[\frac{Nu}{Re^{0.8} \cdot Pr^{1/3}} = \frac{Sh}{Re^{0.8} \cdot Sc^{1/3}} = C\]
where:
- Nu is the Nusselt number
- Sh is the Sherwood number
- Re is the Reynolds number
- Pr is the Prandtl number
- Sc is the Schmidt number
- C is a constant that depends on the specific flow conditions and geometry.
Note: The Prandtl-Taylor analogy is particularly useful for high Prandtl and Schmidt numbers, which are common in many industrial processes involving viscous fluids or gases.
Resources
- “Transport Phenomena” by R. Byron Bird, Warren E. Stewart, and Edwin N. Lightfoot.
- “Introduction to Chemical Engineering Thermodynamics” by J.M. Smith, H.C. Van Ness, and M.M. Abbott.
- “Mass Transfer Operations” by Robert E. Treybal.
Disclaimer: The Solver provided here is for educational purposes. While efforts ensure accuracy, results may not always reflect real-world scenarios. Verify results with other sources and consult professionals for critical applications. Contact us for any suggestions or corrections.