Table of Contents
In Packed Bed Reactor a fluid flows through a bed of solid catalyst where chemical reaction occurs, the Ergun Equation is useful in designing of these reactor which helps in predicting the pressure drop across the bed. It directly affects the flow distribution, energy requirement and reaction efficiency.
Ergun Equation for Packed Bed
The Ergun equation is developed by Sabri Ergun in 1952 which is used to calculate the pressure drop across a packed bed filled with granular or particulate solids, through which a fluid flows. This equation combines the effects of both viscous and inertial forces to measure the pressure drop for fluid flow through a bed of solid particles.
The Ergun Equation Formula is:
\[\frac{\Delta P}{L} = \frac{150 \, \mu \, (1 – \epsilon)^2 \, v}{\epsilon^3 \, d_p^2 \, \phi^2} + \frac{1.75 \, \rho \, (1 – \epsilon) \, v^2}{\epsilon^3 \, d_p \, \phi} \]
where in SI units:
- \(\Delta P\) is the pressure drop across the bed (Pa or N/m2)
- L is the length of the bed (m)
- \(\mu\) is the dynamic viscosity of the fluid (Pa.s)
- \(\epsilon\) is the void fraction (porosity) of the bed (dimensionless)
- v is the Superficial velocity of the fluid (m/s)
- dp is the average particle diameter (m)
- \(\rho\) is density of the fluid, in Kg/m3
- \(\phi\) is the sphericity of the particles.
- The first term in equation is Viscous (laminar) term i.e \(\frac{150 \, \mu \, (1 – \epsilon)^2 \, v}{\epsilon^3 \, d_p^2 \, \phi^2}\), which dominates at low flow rates (Re<10)
- The second term is the inertial (turbulent) term i.e \(\frac{1.75 \, \rho \, (1 – \epsilon) \, v^2}{\epsilon^3 \, d_p \, \phi}\), which is significant at higher flow rates (Re>1000)
Related: Sphericity Calculator for different shapes
Related: Kick’s Law Calculator
Ergun Equation Calculator
This Ergun Equation Calculator helps user to calculate the pressure drop across a packed bed of particles for gas flow through it. User can input the desired values of particle sphericity, diameter, density, bed porosity, gas flow rate, gas density, viscosity and column dimensions.
Note: User may ignore the particle density values, as it is not used in the calculation of pressure drop, whereas it is used in calculation of minimum fluidization velocity which will be the next part of this calculator.
Note: Common values of Sphericity are provided in the table below, select the suitable value.
Related: Head Loss or Pressure Loss Calculator using Darcy-Weisbach Equation
Related: Hagen-Poiseuille Equation Calculator / Poiseuille’s Law Solver
Ergun Equation Significance
he Ergun Equation is used to calculate the pressure drop in packed bed reactors, where fluids (gases or liquids) flow through a bed of solid particles. This equation combines two components: the viscous (or laminar) flow term and the inertial (or turbulent) flow term.
- For Low Reynold’s Number (Re < 10) viscous term of the Ergun equation becomes significant, the flow is slow, and viscous forces dominate over inertial forces.
- This term alone is referred as Carman-Kozeny equation for laminar flow through a packed bed.
\[\frac{\Delta P}{L} =\frac{150 \, \mu \, (1 – \epsilon)^2 \, v}{\epsilon^3 \, d_p^2 \, \phi^2}\]
- For High Reynold’s Number (Re>1000) inertial term of the Ergun equation becomes significant, where inertial forces become more important than viscous forces.
- This term alone is referred as Burke-Plummer equation for turbulent flow through packed beds.
\[\frac{\Delta P}{L} =\frac{1.75 \, \rho \, (1 – \epsilon) \, v^2}{\epsilon^3 \, d_p \, \phi}\]

The superficial velocity (v) which appears in viscous term having linear dependence and as v2 in the inertial term having quadratic dependence with the pressure drop.
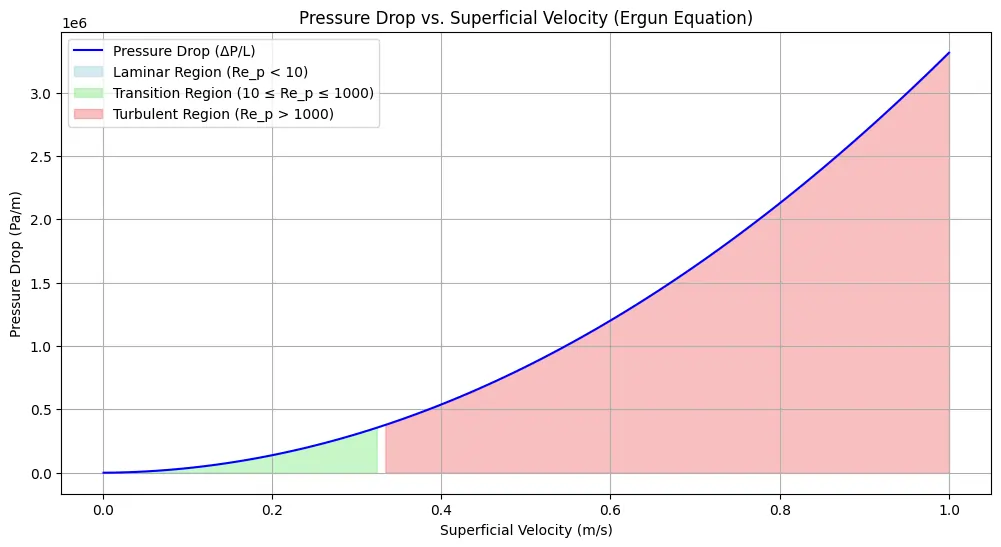
At low velocities, the pressure drop is proportional to v (laminar flow), whereas at high velocities, it is proportional to v2 (turbulent flow). The Ergun equation adjust to the flow regime based on the velocity.
Related: Newton’s Law of Viscosity Calculator – Dynamic Viscosity
Also Read: Area of Cross-Section Calculator for Hollow Sections, Beams & Shapes
Here we are providing the commonly used sphericity values for different particles in the table provided below:
| Particle | Sphericity \(\Psi\) |
|---|---|
| Crushed coal | 0.75 |
| Crushed sandstone | 0.8–0.9 |
| Round sand | 0.92–0.98 |
| Crushed glass | 0.65 |
| Mica flakes | 0.28 |
| Sillimanite | 0.75 |
| Common salt | 0.84 |
Source: Particle characterization for fluidized bed combustion
Related: Sphericity Calculator and formula for Sphere, Cylinder, Cuboid and Irregular Shapes
Must Read: Personal Carbon Footprint Calculator – Track your CO2 Emissions
Example Problem on Ergun Equation using Python
Calculate the pressure drop of air flowing at 30°C and 1 atm through a packed bed composed of spheres with a 1.25 cm diameter. The flow rate of air is 60 kg/min, and the packed bed dimensions are 125 cm in diameter and 250 cm in height. The bed has a porosity of 0.38, while the viscosity and density of air are 0.0182 cP and 0.001156 g/cm³, respectively.
We will be solving this question using python, this will save our time to solve this question:
# Given data
mass_flow_rate = 1 # kg/s
density_air = 1.156 # kg/m^3
viscosity_air = 0.0182e-3 # kg/(m.s)
porosity = 0.38
diameter_bed = 1.25 # m
length_bed = 2.5 # m
diameter_particles = 0.0125 # m
sphericity = 1 # for spheres
# Step 1: Calculate volumetric flow rate (Q)
volumetric_flow_rate = mass_flow_rate / density_air # m^3/s
# Step 2: Calculate superficial velocity (V0)
superficial_velocity = volumetric_flow_rate / ((3.14159 / 4) * diameter_bed**2) # m/s
# Step 3: Calculate particle Reynolds number (NRePM)
reynolds_number = (diameter_particles * superficial_velocity * density_air) / (viscosity_air * (1 - porosity))
# Step 4: Calculate pressure drop (Δp) using Ergun equation
term1 = 150 / reynolds_number
term2 = 1.75
ergun_factor = diameter_particles * porosity**3 / (length_bed * density_air * superficial_velocity**2 * (1 - porosity))
pressure_drop = (term1 + term2) / ergun_factor
# Output the results
print("Volumetric flow rate (Q): {:.3f} m^3/s".format(volumetric_flow_rate))
print("Superficial velocity (V0): {:.3f} m/s".format(superficial_velocity))
print("Particle Reynolds number (NRePM): {:.3f}".format(reynolds_number))
print("Pressure drop (Δp): {:.2f} N/m^2".format(pressure_drop))Output:
Volumetric flow rate (Q): 0.865 m^3/s
Superficial velocity (V0): 0.705 m/s
Particle Reynolds number (NRePM): 902.687
Pressure drop (Δp): 2487.30 N/m^2
Therefore, the pressure drop across the packed bed reactor for the given condition is 2487.30 N/m2
Resources:
- “Unit Operations in Chemical Engineering” (McCabe et al.)
- “Particle Technology and Separation Processes” (Richardson et al.)
- “Chemical Engineering Design: Principles, Practice and Economics of Plant and Process Design” (Towler and Sinnott)
- “Fluid Mechanics: Fundamentals and Applications” by Çengel and Cimbala
Disclaimer: The Solver provided here is for educational purposes. While efforts ensure accuracy, results may not always reflect real-world scenarios. Verify results with other sources and consult professionals for critical applications. Contact us for any suggestions or corrections.