In the field of chemical engineering, dimensionless numbers play an important role in simplifying complex physical phenomena. These numbers are derived from fundamental physical properties.
Here in this article, we will learn 10 mostly used dimensionless numbers in chemical engineering, their definitions, formulas, and practical applications.
Dimensionless Numbers – Quick View
What are Dimensionless Numbers?
Dimensionless Number is the quantity with no units. These numbers are used in Science and Engineering which helps in simplifying complex physical phenomenon by reducing the number of variables.
These dimensionless numbers help engineers and scientists to scale up processes, optimize operations, and enhance the understanding of fluid dynamics, heat transfer, and mass transfer.
| Dimensionless Number | Formula | Interpretation |
|---|---|---|
| Reynolds Number (Re) | \[ Re = \frac{\rho V D}{\mu} \] | Ratio of inertial forces to viscous forces |
| Prandtl Number (Pr) | \[\text{Pr} = \frac{\nu}{\alpha} = \frac{\mu \, C_p}{k}\] | Ratio of momentum diffusivity to thermal diffusivity |
| Nusselt Number (Nu) | \[ Nu = \frac{hL}{k} \] | Ratio of conductive heat flow to convective heat flow |
| Schmidt Number (Sc) | \[ \mathrm{Sc} = \frac{\nu}{D} = \frac{\mu}{\rho D}\] | Ratio of momentum diffusivity to mass diffusivity |
| Sherwood Number (Sh) | \[\text{Sh} = \frac{k_L L}{D} \] | Ratio of mass convection to mass diffusion |
| Damköhler Number (Da) | \[\text{Da} = \frac{k C_0^{n-1} L}{v}\] | Ratio of reaction rate to flow rate |
| Peclet Number (Pe) | \[\text{Pe} = \frac{u L}{D}\] | Ratio of advective transport rate to diffusive transport rate |
| Biot Number (Bi) | \[Bi = \frac{hL_c}{k}\] | Ratio of internal thermal resistance to external convective resistance |
| Froude Number (Fr) | \[\text{Fr} = \frac{U}{\sqrt{gL}}\] | Ratio of inertial force to gravitational force |
| Fourier Number (Fo) | \[\text{Fo} = \frac{\alpha t}{L^2}\] | Ratio of conductive heat transfer rate to heat storage rate |
Reynolds Number (Re)
Reynolds Number is the dimensionless number used in fluid mechanics which is defined as the ratio of inertial forces to viscous forces within a fluid flow.
The formula for Reynolds number is given by:
\[\text{Re} = \frac {\text{Inertial Force}} {\text{viscous Force}}\]
\[ Re = \frac{\rho V D}{\mu} \]
where:
- \( Re \) is the Reynolds number
- \( \rho \) is the density of the fluid
- \( V \) is the velocity of flow
- \( D \) is the pipe diameter
- \( \mu \) is the viscosity of the fluid
For the circular pipe, if Re calculated is high (greater than 2000), then the flow through the pipe is said to be turbulent. If Re is low (less than 2000), the flow is said to be laminar.
Related: Reynolds Number Calculator for a Circular Pipe
Related: Newton’s Law of Viscosity Calculator – Dynamic Viscosity
Related: Hagen-Poiseuille Equation Calculator / Poiseuille’s Law Solver
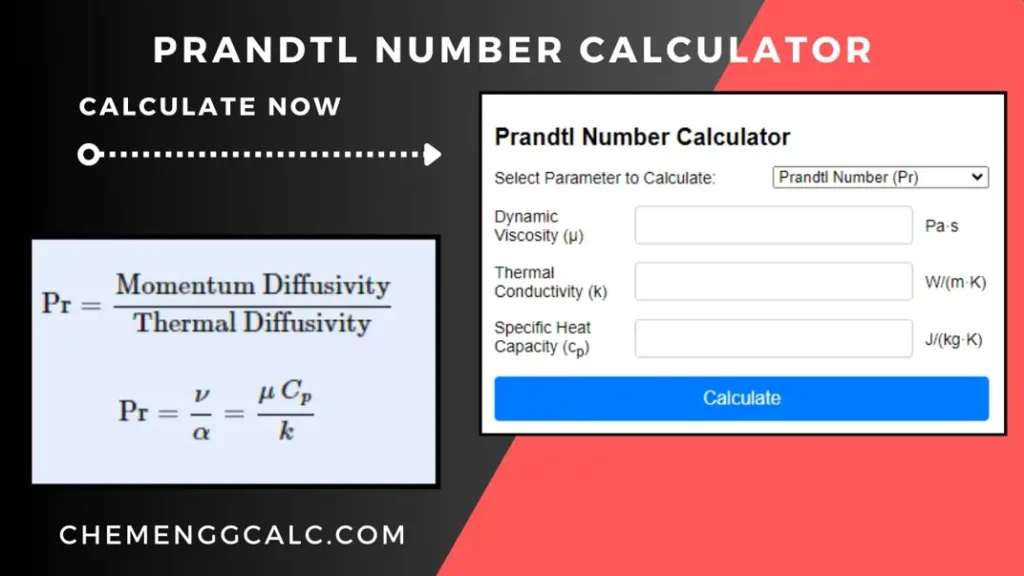
Prandtl Number (Pr)
Prandtl Number (Pr) is the dimensionless number which relates rate of momentum diffusion (viscous diffusion) to the rate of thermal diffusion. This dimensionless number gives the relationship between kinematic viscosity and thermal diffusivity of the fluid.
Mathematically, the Prandtl number is given by:
\[\text{Pr} = \frac {\text{Momentum Diffusivity}} {\text{Thermal Diffusivity}}\]
\[\text{Pr} = \frac{\nu}{\alpha} = \frac{\mu \, C_p}{k}\]
where:
- \(\nu\) is the momentum diffusivity (kinematic viscosity) (m²/s)
- \(\alpha\) is the thermal diffusivity (m²/s)
- \(\mu\) is the dynamic viscosity (N·s/m²)
- \(C_p\) is the specific heat (J/kg·K)
- \(k\) is the thermal conductivity (W/m·K)
Prandtl Number is significant in explaining the relation between relative thickness of the velocity and thermal boundary layers.
Related: Inverse Square Law for Radiation
Related: Heat Transfer through Conduction Calculator – Fourier’s law
Nusselt Number (Nu)
The Nusselt number is the dimensionless number used in heat transfer which is defined as the ratio of convective to conductive heat transfer across a fluid boundary.
Mathematically, Nusselt number is defines as:
\[\text{Nu} = \frac {\text{Conductive Heat Flow}} {\text{Convective Heat Flow}}\]
\[ Nu = \frac{hL}{k} \]
where:
- \( h \) is the convective heat transfer coefficient (W/m²·K),
- \( L \) is a characteristic length (m),
- \( k \) is the thermal conductivity of the fluid (W/m·K).
The Nusselt number (\(𝑁𝑢\)) is significant in the study of heat transfer because it provides a measure of the efficiency of convective heat transfer relative to conductive heat transfer.
Related: Nusselt Number Calculator – Significance and Calculation
Related: Other Heat Transfer Calculators
Schmidt Number (Sc)
The Schmidt number \((Sc)\) is a dimensionless number used in Mass Transfer and it is defined as the ratio of momentum diffusivity (kinematic viscosity) and mass diffusivity.
Mathematically, Schmidt Number it is defined as:
\[Sc = \frac{\text{momentum diffusivity}}{\text{mass diffusivity}} \]
\[ \mathrm{Sc} = \frac{\nu}{D} = \frac{\mu}{\rho D}\]
where (in SI units):
- \( \nu = \frac{\mu}{\rho}\) is the kinematic viscosity (\({m^2/s}\))
- \( D\) is the mass diffusivity (\({m^2/s}\))
- \(\mu\) is the dynamic viscosity (N·s/m²)
- \(\rho\) is the density (Kg/m3)
Note: The heat transfer analogy of the Schmidt number is the Prandtl number (Pr).
The Schmidt number is significant in Mass Transfer provides a measure of the relative rates of momentum and mass transport by diffusion in a fluid.
Related: Schmidt Number Calculator – Significance and Calculation
Related: Fick’s First Law of Diffusion Calculator – Molecular Diffusion
Related: Fick’s Second Law of Diffusion – Concept and Calculation
Sherwood Number (Sh)
Sherwood Number (Sh) is the dimensionless number which is defined as the ratio of convective mass transport to the diffusive mass transport.
Sherwood Number formula is given as:
\[Sh = \frac{\text{Mass Convection}}{\text{mass diffusion}} \]
\[\text{Sh} = \frac{k_L L}{D} \]
where,
- \(k_L\) is the Mass transfer coefficient \(\left( \frac{\text{m}}{\text{s}} \right)\)
- \(L\) is the Characteristic length (m)
- \(D\) is the Mass Diffusivity (\({m^2/s}\))
Note: The Sherwood Number for Mass Transfer is analogous to the Nusselt Number for Heat Transfer.
Sherwood Number is significant in the study of concentration boundary layers.
Related: Thermal Boundary Layer Thickness (δT) for Flat Plate
Damköhler Number (Da)
Damköhler number (Da) is the dimensionless number which compares the reaction rate to the mass transfer rate in the chemical reaction. This number is is important in chemical reaction engineering to determine the dominance of reaction kinetics or mass transport.
For a reaction Damköhler number (Da) is given by:
\[\text{Da} = \frac{k C_0^{n-1} L}{v}\]
where,
- \( k \) is the Reaction rate constant \(\left( \frac{1}{\text{s}} \right)\)
- \( C_0 \) is the Initial concentration \(\left( \frac{\text{mol}}{\text{m}^3} \right)\)
- \( L \) is the Characteristic length \(\left( \text{m} \right)\)
- \( v \) is the Velocity \(\left( \frac{\text{m}}{\text{s}} \right)\)
- \( n \) is order of reaction (dimensionless)
Related: Performance Equation for Ideal Batch Reactor
Related: Rate Constant Calculation using Arrhenius Equation Calculator
Peclet Number (Pe)
The Péclet number describes the relative importance of advection to diffusion in transport phenomena.
The formula of Peclet Number is gives as:
\[Pe = \frac{\text{Advective Transport Rate}}{\text{Diffusive Transport Rate}} \]
\[\text{Pe} = \frac{u L}{D}\]
where,
- \( u\) is the flow velocity (m/s)
- \( L \) is the Characteristic length (m)
- \( D \) is the Diffusivity (m2/s)
Peclet Number is important in analyzing the transport of heat or mass in the flowing fluids. A high Péclet number means advection (bulk transport) dominates over diffusion. Whereas, a low Péclet number means diffusion is the dominant transport mechanism.
Related: Fick’s second law of Diffusion
Biot Number (Bi)
Biot Number (Bi) is a dimensionless number and defined as internal thermal resistance within a body (conduction) to the external thermal resistance due to convection.
Biot Number formula is given as:
\[Bi = \frac{\text{Internal Thermal Resistance}}{\text{External convective Resistance}}\]
\[Bi = \frac{R_{\text{Conduction}}}{R_{\text{convection}}} = \frac{hL_c}{k}\]
where:
- \( h \) is the convective heat transfer coefficient (W/m2·K)
- \(L_c \) is the characteristic length (m)
- \( k \) is the thermal conductivity of the material (W/m·K)
The Biot number provides a measure of the temperature drop in the solid relative to the temperature difference between the surface and the fluid.
Related: Biot Number Calculator – Significance and Calculations
Related: Hydraulic Diameter Calculator for Circular and Non-Circular cross-section
Related: Inverse Square Law for Radiation
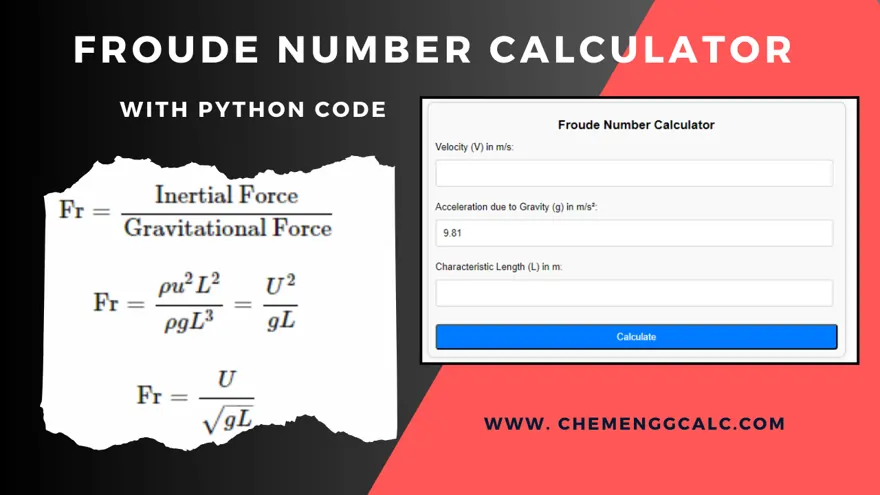
Froude Number (Fr)
The Froude number is defined as the ratio of inertia force to the gravitational forces in fluid dynamics.
Mathematically, Froude Number is defined as:
\[\text{Fr} =\frac{\text{Inertial Force}}{\text{Gravitational Force}}\]
\[\text{Fr} = \frac{U}{\sqrt{gL}}\]
where:
- \(U\) is the characteristic velocity of the flow
- \(g\) is the acceleration due to gravity
- \(L\) is the characteristic length
Froude number is important in the study of open channel flows, ship hydrodynamics, and the behavior of flow around objects.
Related: Froude Number Calculator – Significance and Applications
Related: Newton’s Law of Viscosity Calculator – Dynamic Viscosity
Related: Hagen-Poiseuille Equation Calculator / Poiseuille’s Law Solver
Fourier Number (Fo)
Fourier Number (Fo) is the dimensionless time and defined as the ratio of the heat conduction rate to the rate of thermal energy storage in a solid.
The formula for Fourier Number is given as:
\[\text{Fo} = \frac{\alpha t}{L^2}\]
- \(\alpha \) is the thermal diffusivity (m2/s)
- \( t \) is the time (s)
- \( L \) is the Characteristic length (m)
Fourier Number is used to determine the distribution of temperature within a material over time. A high Fourier number means heat has diffused rapidly as compare to the time scale i.e efficient heat conduction. Whereas A Low Fourier Number means heat conduction is slow relative to the time scale.
Related: Kirchoff’s Law of Thermal Radiation, Wien’s Displacement Law – Concept and Calculations
Related: Convective Heat Transfer Calculator – Newton’s Law of Cooling

Resources
- “Fundamentals of Heat and Mass Transfer” by Theodore L. Bergman, Adrienne S. Lavine, Frank P. Incropera, and David P. DeWitt.
- “Heat Transfer Book” by David W. Hahn.
- “Chemical Reaction Engineering“ by Octave Levenspiel
- “Thermodynamics: An Engineering Approach” by Yunus A. Çengel and Michael A. Boles
Disclaimer: The content provided here is for educational purposes. While efforts ensure accuracy, results may not always reflect real-world scenarios. Verify results with other sources and consult professionals for critical applications. Contact us for any suggestions or corrections.