Table of Contents
The critical speed of a ball mill is an important concept in milling and grinding operation for size reduction. Ball mill enhances efficiency, reduces wear on the mill components, and minimizes energy consumption, therefore improves the overall productivity in various industrial processes.
What is Critical Speed of a Ball Mill?
The critical speed of a ball mill is the rotational speed at which the centrifugal forces acting on the ball are equal to the gravitational force. At this speed the outermost balls loose the contact with the wall of the mill and ready to fall. The critical speed can be calculated using the formula:
\[N_c = \frac{1}{2\pi} \sqrt{\frac{g}{R – r}}\]
where in S.I units,
- Nc is the critical speed in revolutions per second (rps or rpm)
- g is acceleration due to gravity (9.81 m/s²)
- R is the radius of the mill (m)
- r is the radius of the ball (m)
Note: If the mill operates below the critical speed, the balls fall back down onto the material to be ground by impact and attrition. If the mill operates above the critical speed, the balls are carried around with the mill and do not fall back, which reduces the grinding effectiveness.
Critical Speed of a Ball Mill Calculator
This critical speed calculator of a ball mill helps user to determine the critical rotational speed in rpm, which is essential for efficient grinding. User can input the values of the radius of the mill, the radius of the balls. This web tool are having interactive sliders for adjusting the radii and real-time results are updated.
Related: Sphericity Calculator for different shapes
Related: Kick’s Law Calculator and Bond’s Law Calculator and Work Index
Working Principle of a Ball Mill
A ball mill operates on the principle of impact and attrition. It consists of a rotating cylindrical drum partially filled with grinding media, such as steel balls, ceramic balls, or rods.
As the drum rotates, the grinding media (usually balls) are picked up by the mill and carried nearly to the top where they break contact with the wall and fall to the bottom to be picked up again.
Centrifugal force which is applied due to rotational movement, keeps the grinding media intact with the wall during the upward movement and then cascade or fall onto the material causing grinding by slipping and rolling over each other, thus causes results in breaking down of material.
his process combines both impact forces, where the grinding media collide with the material, and attrition forces, where the material is ground down by the friction between the media and the drum. The size of the final product is controlled by the rotation speed of the drum, the size of the media, and the duration of grinding.
Related: More Mechanical Operation Calculators
Related: Cake Filtration – Calculation for Filter Medium and Specific Cake Resistance
Derivation for Critical Speed of a Ball Mill
In a ball mill, the forces acting on a ball at any point include gravitational force and centrifugal force. At the critical speed, the ball will not fall back into the mill but will be pinned (ready to fall) to the mill wall due to these forces.
The gravitational force acting downward is given by:
\[F_g = \frac{mg}{g_c}\]
where ( m ) is the mass of the ball and ( g ) is the acceleration due to gravity.
The centrifugal force acting outward is given by:
\[F_c = \frac{mu^2}{(R – r)g_c}\]
where ( u ) is the velocity of the ball, ( R ) is the radius of the mill, and ( r ) is the radius of the ball.
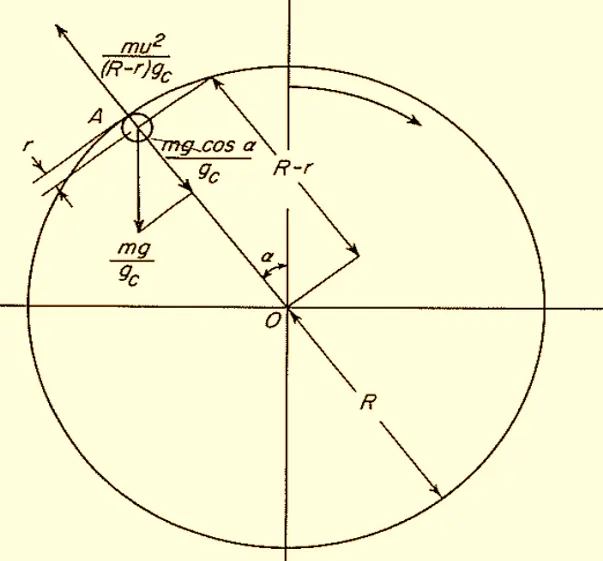
At the critical speed, the centrifugal force equals the gravitational force. Putting these forces equal gives:
\[\frac{mu^2}{(R – r)g_c} = \frac{mg}{g_c} \cdot \cos{\alpha}\]
where \( \alpha \) is the angle at which the ball is located. In S.I units \((g_c = 1)\), it is used to make the units consistent, here we are using consistent units.
At the top of the mill, \( \alpha = 0 \), which gives \( \cos{\alpha} = 1 \). therefore, the equation simplifies to:
\[\frac{mu^2}{(R – r)g_c} = \frac{mg}{g_c}\]
Solving the equation for velocity ( u ) and then taking the roots both side, we get:
\[u^2 = g \cdot (R – r)\]
\[u = \sqrt{g \cdot (R – r)}\]
The velocity ( u ) can also be expressed in terms of the angular velocity \( \omega \) as \(u = \omega \cdot (R – r)\)
Substituting this into the equation for ( u ), we get:
\[\omega \cdot (R – r) = \sqrt{g \cdot (R – r)}\]
Solving for the angular velocity \( \omega \) and the critical speed \(N_c\) in revolution per second is related to angular velocity by \(N_c = \frac{\omega}{2\pi}\)
\[\omega = \frac{\sqrt{g \cdot (R – r)}}{R – r}\]
now, substituting the expression for \( \omega \), we get the final expression:
\[N_c = \frac{1}{2\pi} \cdot \frac{\sqrt{g}}{\sqrt{R – r}}\]
Therefore, the critical speed of the ball mill is given by:
\[N_c = \frac{1}{2\pi} \sqrt{\frac{g}{R – r}}\]
Related: Darcy’s Law Calculation for flow through porous media – Assumption & Applications
Python Code for Critical Speed of a Ball Mill
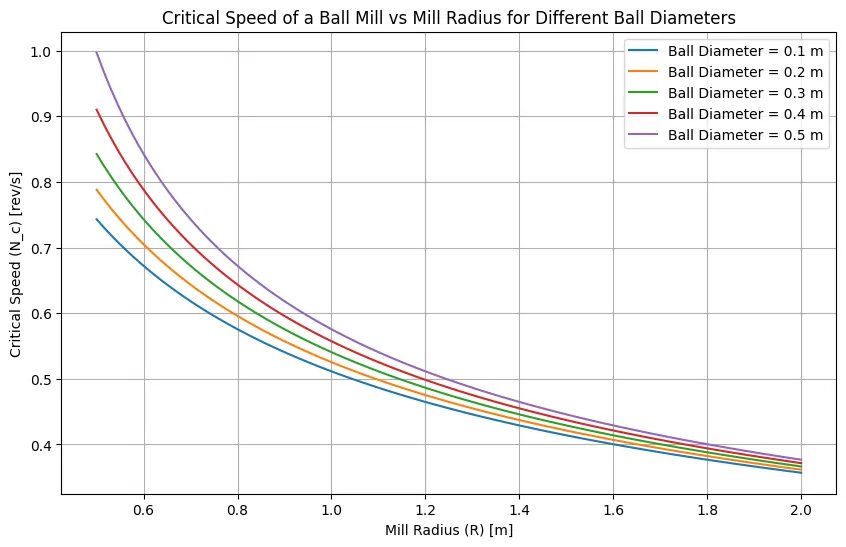
This Python code helps user to calculate the critical speed of a ball mill for different ball diameters. It uses the formula for critical speed, which depends on the mill radius and ball diameter, and evaluates this speed for a range of mill radii in rotation per second.
Note: This Python code solves the specified problem. Users can copy the code and run it in a suitable Python environment. By adjusting the input parameters, users can observe how the output changes accordingly.
import numpy as np
import matplotlib.pyplot as plt
# Constants
g = 9.81 # Acceleration due to gravity (m/s^2)
# Function to calculate critical speed for different ball diameters
def critical_speed_different_balls(g, R, r):
return (1 / (2 * np.pi)) * np.sqrt(g / (R - r))
# Radius of the mill (R) values
R_values = np.linspace(0.5, 2.0, 100) # Mill radius from 0.5m to 2.0m
# Different ball radii (in meters)
r_values = [0.05, 0.1, 0.15, 0.2, 0.25] # Ball radii
# Plotting the results for different ball diameters
plt.figure(figsize=(10, 6))
for r in r_values:
N_c_values = critical_speed_different_balls(g, R_values, r)
plt.plot(R_values, N_c_values, label=f"Ball Diameter = {2*r} m")
plt.xlabel("Mill Radius (R) [m]")
plt.ylabel("Critical Speed (N_c) [rev/s]")
plt.title("Critical Speed of a Ball Mill vs Mill Radius for Different Ball Diameters")
plt.grid(True)
plt.legend()
plt.show()
Output:
Resources
- “Unit Operations in Chemical Engineering” (McCabe et al.)
- “Particle Technology and Separation Processes” (Richardson et al.)
- “Chemical Engineering Design: Principles, Practice and Economics of Plant and Process Design” (Towler and Sinnott)
Disclaimer: The Solver provided here is for educational purposes. While efforts ensure accuracy, results may not always reflect real-world scenarios. Verify results with other sources and consult professionals for critical applications. Contact us for any suggestions or corrections.