Clausius Clapeyron Equation Calculator, Derivation and Applications

What is Clausius Clapeyron Equation / Relation?

The Clausius Clapeyron equation is a relation in thermodynamics that describes the phase transition between two phases of matter, such as between liquid and vapor for a pure substance. This equation calculates the change in vapor pressure with temperature which is useful in predicting the behavior of substances undergoing phase transitions.

Differential form of Clausius Clapeyron Equation is written as:

\[ \frac{dP}{dT} = \frac{\Delta H_{\text{vap}}}{T \Delta V} \]

where in S.I. units,

• \( \frac{dP}{dT}\) is the rate of change of pressure with respect to temperature (measured in \(\text{Pa/K}\) i.e Pascals per Kelvin
• \(\Delta H_{\text{vap}}\) or \(L\) is the enthalpy of vaporization (measured in \(\text{J/mol}\) i.e Joule per mole.
• \(T\) is the absolute temperature (measured in Kelvin)
• \(\Delta V\) is the change in volume during the phase transition (measured in m3/mol i.e cubic meters per mole)

Integral form of Clausius Clapeyron Equation is written as:

\[ \ln \left( \frac{P_1}{P_2} \right) = \frac{\Delta H_{\text{vap}}}{R} \left( \frac{1}{T_2} – \frac{1}{T_1} \right) \]

where,

• \(P_1\)​ and \(P_2\) are the Vapor pressures at temperatures \(T_1\)​ and \(T_2\) respectively
• \(\Delta H_{\text{vap}}\) is the enthalpy of vaporization.
• \(R\) is the Universal gas constant

Related: Kirchoff’s Law of Thermal Radiation, Wien’s Displacement Law

Related: Joule-Thomson Effect – Coefficient Calculation for CO2 and N2

Clausius Clapeyron Equation Calculator

This web tool/Calculator helps user to calculate one of three parameters related to phase changes using integrated form of Clausius Clapeyron Equation \( \ln \left( \frac{P_1}{P_2} \right) = \frac{\Delta H_{\text{vap}}}{R} \left( \frac{1}{T_2} – \frac{1}{T_1} \right) \). User can select the desired parameters to calculated based on the given drop down and required input fields will open on selection of parameter.

Related: Hydraulic Diameter Calculator for Circular and Non-Circular cross-section

Related: Inverse Square Law for Radiation

Clausius-Clapeyron Equation Derivation

The Clausius-Clapeyron equation can be derived from thermodynamics principles. At equilibrium, the Gibbs free energy (\( G \)) of the two phases is equal. The change in Gibbs free energy (\( dG \)) is given by:

\(dG = V dP – S dT\)

For a phase transition at equilibrium between the liquid and vapor phases i.e infinitesimal changes in Gibbs free energy for the vapor and liquid phases are equal.

\(dG_{\text{vapor}} = dG_{\text{liquid}}\)

Thus, putting the values of dG for both liquid and vapor phase

\(V_{\text{vapor}} dP – S_{\text{vapor}} dT\) = \( V_{\text{liquid}} dP – S_{\text{liquid}} dT\)

Rearranging this, we get:

\((V_{\text{vapor}} – V_{\text{liquid}}) dP\) = \((S_{\text{vapor}} – S_{\text{liquid}}) dT\)

The latent heat (\( L \)) of the phase transition is related to the entropy change (\( \Delta S \)) by:

\(L = T \Delta S\)

Therefore, the change in entropy is:

\(\Delta S = \frac{L}{T}\)

Substituting \( \Delta S \) and \( \Delta V \) into the thermodynamic identity, we get

\((V_{\text{vapor}} – V_{\text{liquid}}) dP = \frac{L}{T} dT\)

Let \( \Delta V = V_{\text{vapor}} – V_{\text{liquid}} \), we get

\(\frac{dP}{dT} = \frac{L}{T \Delta V}\)

This equation is the differential form of the Clausius Clapeyron equation. This form gives the rate of change of pressure with temperature for a phase transition (applicable for all phase transformation).

Now, To derive the Integral form, assuming vapor behaves as an ideal gas, volume in vapor phase is much greater than volume in liquid phase i.e \((V_{\text{vapor}} >> V_{\text{liquid}})\)

therefore, \(\Delta V \approx V_{\text{vapor}} = \frac{RT}{P}\)

Substituting this into the differential form, we get

\(\frac{dP}{dT} = \frac{L}{T \left( \frac{RT}{P} \right)} = \frac{LP}{RT^2}\)

on rearranging and integrating both sides, we get

\(\int_{P_1}^{P_2} \frac{dP}{P} = \frac{L}{R} \int_{T_1}^{T_2} \frac{dT}{T^2}\)

performing integration both side, we get:

\(\ln \left( \frac{P_2}{P_1} \right) = -\frac{L}{R} \left( \frac{1}{T_2} – \frac{1}{T_1} \right)\)

above equation can be rewritten as:

\( \ln \left( \frac{P_1}{P_2} \right) = \frac{\Delta H_{\text{vap}}}{R} \left( \frac{1}{T_2} – \frac{1}{T_1} \right) \)

This is the integrated form of the Clausius Clapeyron equation. This form relates the pressures and temperatures at two different states along the phase transition boundary, assuming ideal gas behavior for the vapor phase.

The extended formula for Clausius Clapeyron equation where Antoine Equation is determined.

Related: Click here to learn more about Antoine Equation

Example Problem on Clausius Clapeyron Equation

Calculate the enthalpy of vaporization \(( \Delta H_{\text{vap}} )\) for ethanol, given the vapor pressure at 40 \(^\circ\)C is 150 torr. The normal boiling point for ethanol is 78\(^\circ\)C.

Here, we have give two sets of \((P, T)\) data:

• At 150 torr given temperature is 40+273 = 313K
• At 760 torr i.e at normal boiling point, given temperature is 78+273 = 351K

For the given set of data, using Clausius-Clapeyron equation:

\(\ln \left( \frac{P_1}{P_2} \right) = \frac{-\Delta H_{\text{vap}}}{R} \left( \frac{1}{T_1} – \frac{1}{T_2} \right)\)

Substituting the given values, we get

\(\ln \left( \frac{150}{760} \right) = \frac{-\Delta H_{\text{vap}}}{8.314} \left( \frac{1}{313} – \frac{1}{351} \right)\)

Solving for \( \Delta H_{\text{vap}} \)

\(\Delta H_{\text{vap}} = \frac{1.623 \times 8.314}{0.000345} = 39107 \frac{J}{mol}\)

\(\Delta H_{\text{vap}} \approx 3.90 \times 10^4 \ \text{J/mol}\)

Thus, the enthalpy of vaporization \(( \Delta H_{\text{vap}} )\) for ethanol is approximately \( 3.90 \times 10^4 \) joules per mole.

Application of Clausius Clapeyron Equation

1. In Meteorology, it is used to understand cloud formation and precipitation patterns by relating temperature variations to changes in water vapor pressure.
2. For the equipment design like boilers, condensers, and refrigeration systems, the Clausius Clapeyron equation is used to analyze phase change processes and ensure the systems operate efficiently and safely.
3. This equation helps in modelling the evaporation rates of pollutants and other volatile organic compounds, which is important to understand the environmental impacts and can be used pollution control.
4. In Pharmaceutical and Food Science, this equation can be used to determine the stability and shelf-life by understanding how changes in temperature affect the vapor pressure and phase transitions of these substances.

Python Code for Clausius Clapeyron Equation

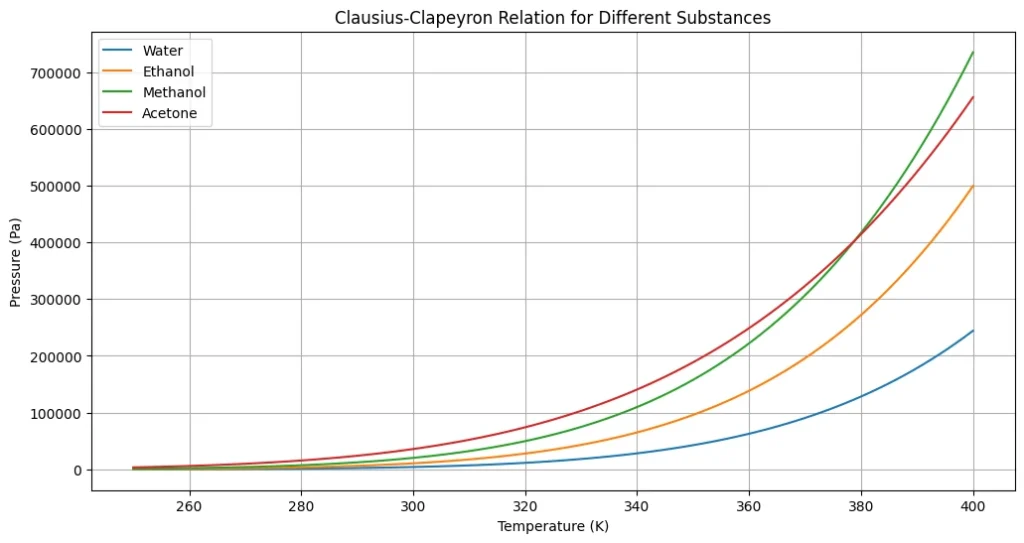
This Python code helps user to understand the pressure-temperature relationship for different substances using the Clausius Clapeyron equation for water, ethanol, methanol, and acetone.

Note: This Python code solves the specified problem. Users can copy the code and run it in a suitable Python environment. By adjusting the input parameters, users can observe how the output changes accordingly.

import numpy as np
import matplotlib.pyplot as plt

def clausius_clapeyron(P1, T1, T2, L, R=8.314):
    """
    Calculate the pressure at temperature T2 using the Clausius-Clapeyron equation.
    
    Parameters:
    P1 (float): Initial pressure (in Pa)
    T1 (float): Initial temperature (in K)
    T2 (float): Final temperature (in K)
    L (float): Latent heat (in J/mol)
    R (float): Universal gas constant (default is 8.314 J/(mol·K))
    
    Returns:
    float: Pressure at temperature T2 (in Pa)
    """
    return P1 * np.exp(-L/R * (1/T2 - 1/T1))

# Parameters for different substances
substances = {
    'Water': {
        'P1': 101325,     # Pressure at T1 (1 atm in Pa)
        'T1': 373.15,     # Boiling point of water (in K)
        'L': 40660        # Latent heat of vaporization for water (in J/mol)
    },
    'Ethanol': {
        'P1': 101325,     # Pressure at T1 (1 atm in Pa)
        'T1': 351.44,     # Boiling point of ethanol (in K)
        'L': 38390        # Latent heat of vaporization for ethanol (in J/mol)
    },
    'Methanol': {
        'P1': 101325,     # Pressure at T1 (1 atm in Pa)
        'T1': 337.85,     # Boiling point of methanol (in K)
        'L': 35820        # Latent heat of vaporization for methanol (in J/mol)
    },
    'Acetone': {
        'P1': 101325,     # Pressure at T1 (1 atm in Pa)
        'T1': 329.45,     # Boiling point of acetone (in K)
        'L': 29000        # Latent heat of vaporization for acetone (in J/mol)
    }
}

T_min = 250  # Minimum temperature (in K)
T_max = 400  # Maximum temperature (in K)
num_points = 100  # Number of points in the plot

# Generate temperature values
temperatures = np.linspace(T_min, T_max, num_points)

# Create the plot
plt.figure(figsize=(12, 6))

# Plot for each substance
for substance, params in substances.items():
    P1 = params['P1']
    T1 = params['T1']
    L = params['L']
    
    # Calculate pressure values
    pressures = clausius_clapeyron(P1, T1, temperatures, L)
    
    # Plot
    plt.plot(temperatures, pressures, label=f'{substance}')

# Customize the plot
plt.xlabel('Temperature (K)')
plt.ylabel('Pressure (Pa)')
plt.title('Clausius-Clapeyron Relation for Different Substances')
plt.legend()
plt.grid(True)
plt.show()

Output:

Resources

• “Thermodynamics: An Engineering Approach” by Yunus A. Çengel and Michael A. Boles
• “Introduction to Chemical Engineering Thermodynamics” by J.M. Smith, H.C. Van Ness, and M.M. Abbott
• NPTEL Lectures on Thermodynamics

Disclaimer: The Solver provided here is for educational purposes. While efforts ensure accuracy, results may not always reflect real-world scenarios. Verify results with other sources and consult professionals for critical applications. Contact us for any suggestions or corrections.