Table of Contents
Average particle size is a fundamental parameter that provide dimensions of particles in a given sample and plays an important role in determining the physical and chemical properties of materials.
There are several methods to calculate average particle size, each of these methods provides unique insights into the particle distribution of a sample. These methods include the Volume-Surface Mean Diameter, Arithmetic Mean Diameter, Mass Mean Diameter, and Volume Mean Diameter.
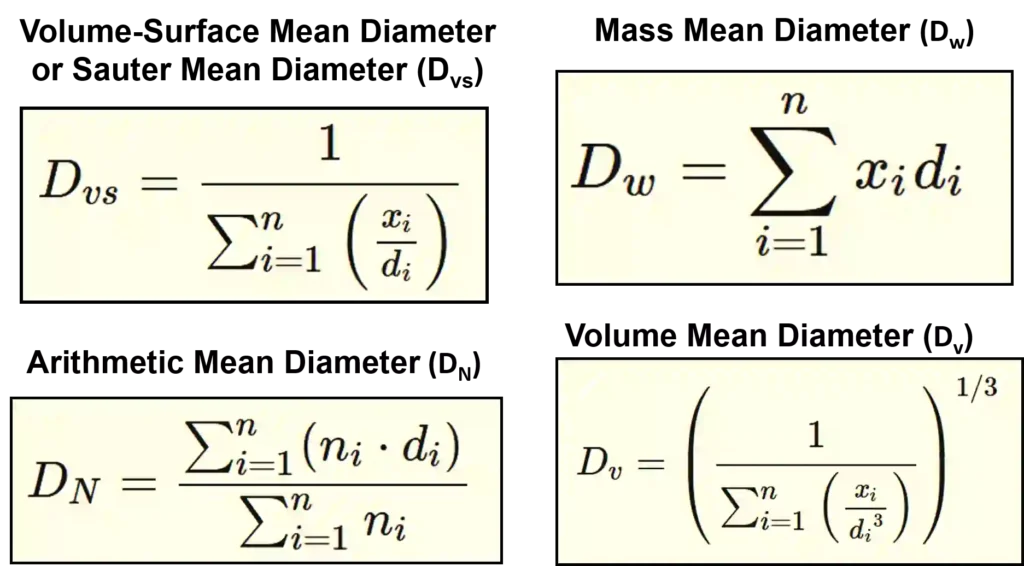
Related: Sphericity Calculator for different shapes
Related: Ergun Equation Calculator for Pressure Drop in Packed Bed Column
Specific Surface of Mixtures
The specific surface area (SSA) of a mixture of particles is a measure of the total surface area of the particles per unit mass or volume of the mixture.
To determine the specific surface area of a mixture of particles, assuming the sphericity (\(\phi\)), density of particle (\(\rho\)) be constant, therefore the total surface area per unit mass of the mixture is given as:
\[A_{w,i} = \frac{6 \phi_i}{d_{p,i} \rho_i}\]
For the entire mixture the above formula can be written as:
\[A_w = \sum_{i=1}^{n} x_i A_{w,i} \]
\[A_w = \frac{6 \phi}{\rho} \sum_{i=1}^{n} \left( \frac{x_i}{d_{p,i}} \right)\]
where,
- \(\phi\) is the Sphericity of particles (assuming constant)
- \(d_{p,i}\) is the Diameter of particle \(i\)
- \(x_i\) is the Mass fraction of particle \(i\)
- \(\rho\) is the Density of particles (assuming constant)
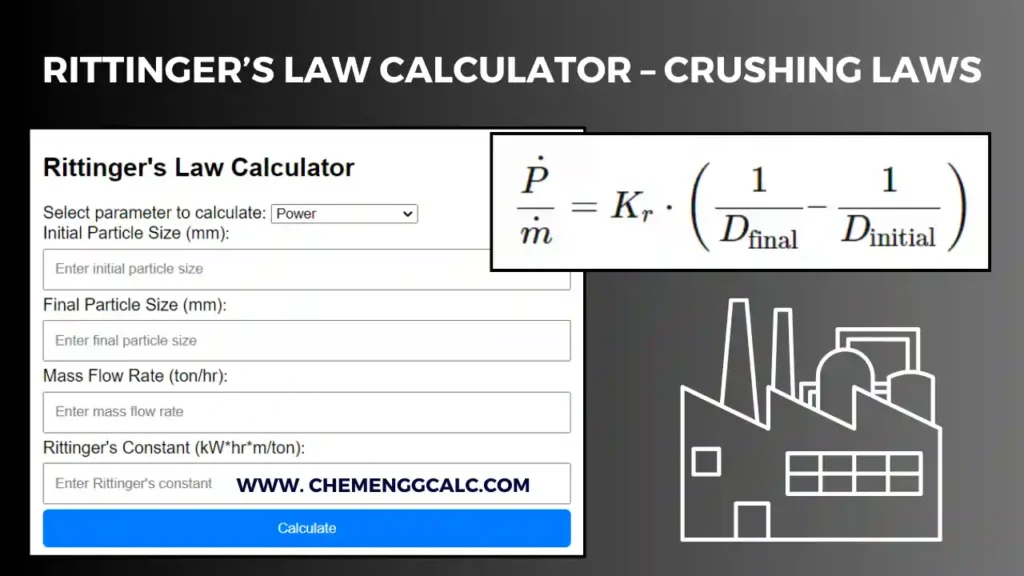
Related: Rittinger’s Law Calculator
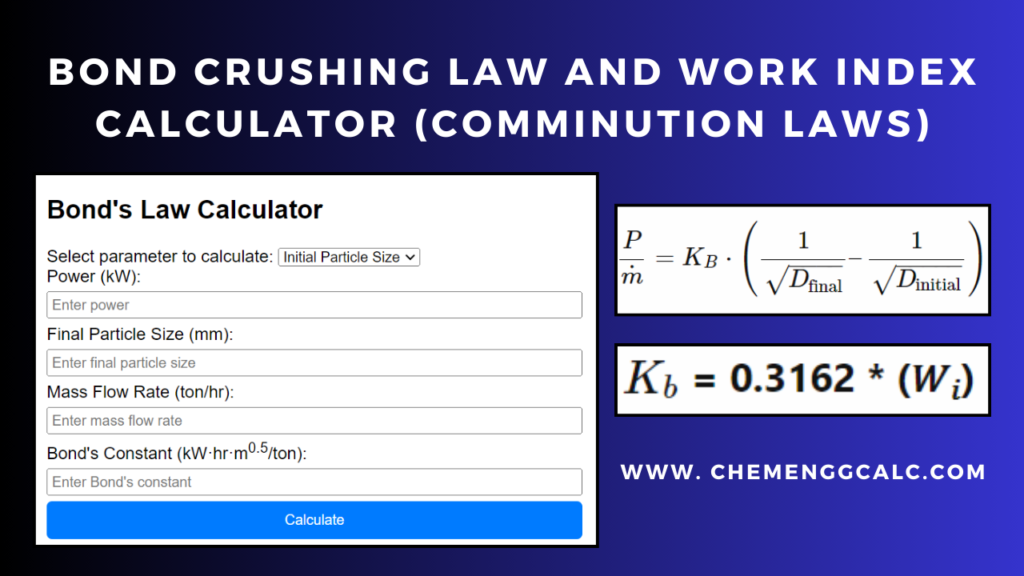
Related: Kick’s Law Calculator
Volume-Surface Mean Diameter (Dvs) or Sauter Mean Diameter
Volume-Surface Mean Diameter also known as Sauter Mean diameter which is the most used method for average particle size calculation, this is significant where the surface area of particles is critical, such as in reactions and dissolution rates.
The formula for the Volume-Surface Mean Diameter \((D_{vs})\) or Sauter Mean Diameter is:
\[D_{vs} = \frac{\sum_{i=1}^{n} n_i d_i^3}{\sum_{i=1}^{n} n_i d_i^2}\]
above equation can be solved further and can be written in terms of mass fraction \(x_i\)
\[ D_{vs} = \frac{1}{\sum_{i=1}^{n} \left( \frac{x_i}{d_i} \right)} \]
where,
- \(d_i\) is the diameter of particle \(i\)
- \(n_i\) is the number of particles of diameter \(d_i\)
- \(x_i\) is the mass fraction of particle of diameter \(d_i\)
Edition: 7th Edition, By: Warren L. McCabe, Julian C. Smith, Peter Harriott
A comprehensive resource on chemical engineering principles, covering core unit operations and practical applications essential for professionals and students alike.
Buy on AmazonArithmetic Mean Diameter (DN)
The Arithmetic Mean Diameter is simply the average of the diameters of all particles. it is significant when the number of particles is more important than their size.
The formula for the Arithmetic Mean Diameter \((D_N)\) is:
\[ D_{N} = \frac{\sum_{i=1}^{n} (n_i \cdot d_i)}{\sum_{i=1}^{n} n_i} \]
the sum of all the particles on can be written as \( \sum_{i=1}^{n} n_i = N\)
\[ D_{N} = \frac{\sum_{i=1}^{n} (n_i \cdot d_i)}{N} \]
where,
- \(d_i\) is the diameter of particle \(i\)
- \(n_i\) is the number of particles of diameter \(d_i\)
- \(N\) is the total number of particles in entire sample
Related: Head Loss or Pressure Loss Calculator using Darcy-Weisbach Equation
Mass Mean Diameter (Dw)
Mass Mean Diameter is simply the sum of mass fraction of individual size multiplied by the diameter. It is significant in processes where mass transfer or weight distribution is important, such as sedimentation and centrifugation.
The formula for the Mass Mean Diameter \((D_w)\) is:
\[ D_{w} = \sum_{i=1}^{n} {x_i}{d_i} \]
where,
- \(d_i\) is the diameter of particle \(i\)
- \(x_i\) is the mass fraction of particle of diameter \(d_i\)
Volume Mean Diameter (Dv)
The Volume Mean Diameter is determined by dividing the total volume of the sample by the number of particles in the mixture which gives the average volume of the particle. This diameter is significant in processes where volume or space occupied by particles matters, like packing and storage.
The formula for the Volume Mean Diameter \((D_v)\) is:
\[ D_{v} = \left( \frac{1}{\sum_{i=1}^{n} \left( \frac{x_i}{{d_i}^3} \right)}\right)^{1/3} \]
where,
- \(d_i\) is the diameter of particle \(i\)
- \(n_i\) is the number of particles of diameter \(d_i\)
- \(x_i\) is the mass fraction of particle of diameter \(d_i\)
Note: For uniform particle size, all the diameters mentioned above are same. For mixture containing the particle on various sizes these diameters can be used for specific cases.
| Average Particle Diameters | Diameter Formula |
|---|---|
| Volume-Surface Mean Diameter or Sauter Mean Diameter | \[D_{vs} = \frac{\sum_{i=1}^{n} n_i d_i^3}{\sum_{i=1}^{n} n_i d_i^2}\] or \[ D_{vs} = \frac{1}{\sum_{i=1}^{n} \left( \frac{x_i}{d_i} \right)} \] |
| Arithmetic Mean Diameter | \[ D_{N} = \frac{\sum_{i=1}^{n} (n_i \cdot d_i)}{N} \] |
| Mass Mean Diameter | \[ D_{w} = \sum_{i=1}^{n} {x_i}{d_i} \] |
| Volume Mean Diameter | \[ D_{v} = \left( \frac{1}{\sum_{i=1}^{n} \left( \frac{x_i}{{d_i}^3} \right)}\right)^{1/3} \] |
Number of Particles in the Mixture
Number of Particles (\(N_w\)) in the mixture can be calculated from the differential analysis in each fraction, it is the total population in one mass unit of sample. For a given particle shape factor (\(a\)), the number of particle are given by:
\[N_w = \frac{1}{a \cdot \rho} \sum_{i=1}^{n} \left( \frac{x_i}{d_{p,i}^3} \right)\]
where,
- \(d_{p,i}\) is the Diameter of particle \(i\)
- \(x_i\) is the Mass fraction of particle \(i\)
- \(\rho\) is the Density of particles (assuming constant)
Example Problem on Average Particle Size
The screen analysis in the following table applies to a sample of crushed quartz. The density of the particles is 2650 \(kg/m^3\) and shape factors are \(a = 2\) and \(\phi = 0.571\). For the material between 4 mesh and 200 mesh in particle size calculate, (a) The number of particles per gram (b) volume mean diameter (c) Volume-Surface Mean diameter (d) Mass Mean Diameter
| Mesh | Screen Opening, \(D_i\) in mm | Mass fraction retained, \(x_i\) |
|---|---|---|
| 4 | 4.6990 | 0.0000 |
| 6 | 3.3270 | 0.0251 |
| 8 | 2.3620 | 0.1250 |
| 10 | 1.6510 | 0.3207 |
| 14 | 1.1680 | 0.2570 |
| 20 | 0.8330 | 0.1590 |
| 28 | 0.5890 | 0.0538 |
| 35 | 0.4178 | 0.0210 |
| 48 | 0.2950 | 0.0102 |
| 65 | 0.2080 | 0.0077 |
| 100 | 0.1470 | 0.0058 |
| 150 | 0.1040 | 0.0041 |
| 200 | 0.0740 | 0.0031 |
| Pan | 0.0000 | 0.0075 |
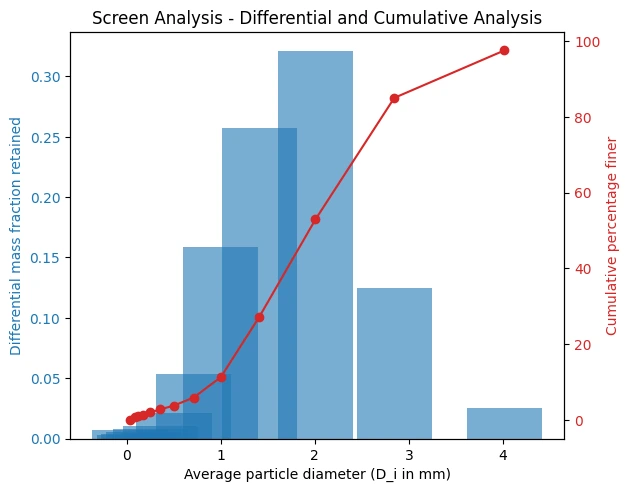
From the given data, first we will calculate the average particle size for i screen and i+1 screen using simple arithmetic mean, for mesh increment size 4/6, the average is calculated as (4.6990 + 3.3270)/ 2 = 4.013 mm, similarly for other increment as shown in table below:
In the next step, for the mesh increment size 4/6, the mass fraction retained, \(x_i\) is 0.0251, therefore the \(\frac{x_i}{d_i}\) and \(\frac{x_i}{{d_i}^3}\) is calculated as shown in the table below:
| Mesh | Screen Opening \(D_i\) in mm | \(x_i\) | Average Size \(D_i\) in mm | \(\frac{x_i}{d_i}\) | \(\frac{x_i}{{d_i}^3}\) |
|---|---|---|---|---|---|
| 4 | 4.6990 | 0.0000 | – | – | – |
| 6 | 3.3270 | 0.0251 | 4.0130 | 0.00625 | 0.0004 |
| 8 | 2.3620 | 0.1250 | 2.8445 | 0.04394 | 0.0054 |
| 10 | 1.6510 | 0.3207 | 2.0065 | 0.15983 | 0.0397 |
| 14 | 1.1680 | 0.2570 | 1.4095 | 0.18233 | 0.0918 |
| 20 | 0.8330 | 0.1590 | 1.0005 | 0.15892 | 0.1588 |
| 28 | 0.5890 | 0.0538 | 0.7110 | 0.07567 | 0.1497 |
| 35 | 0.4178 | 0.0210 | 0.5034 | 0.04172 | 0.1646 |
| 48 | 0.2950 | 0.0102 | 0.3564 | 0.02862 | 0.2253 |
| 65 | 0.2080 | 0.0077 | 0.2515 | 0.03062 | 0.4840 |
| 100 | 0.1470 | 0.0058 | 0.1775 | 0.03268 | 1.0371 |
| 150 | 0.1040 | 0.0041 | 0.1255 | 0.03267 | 2.0742 |
| 200 | 0.0740 | 0.0031 | 0.0890 | 0.03483 | 4.3974 |
| Pan | 0.0000 | 0.0075 | 0.0370 |
From above table, we can calculate the sum of \(\frac{x_i}{d_i}\) and \(\frac{x_i}{{d_i}^3}\).
From the table, \(\sum \frac{x_i}{d_i} = 0.828\) and \(\sum \frac{x_i}{{d_i}^3} = 8.8284\)
a) To calculate the number of particles per gram, we will use formula as
\(N_w = \frac{1}{a \cdot \rho} \sum_{i=1}^{n} \left( \frac{x_i}{d_{p,i}^3} \right)\)
putting the values of \(2650 kg/m^3 = 0.00265 g/mm^3\), shape factors are \(a = 2\) and \(\sum \frac{x_i}{{d_i}^3} = 8.8284\), we get
\(N_w = \frac{1}{2 \cdot 0.00265} \left( 8.8284 \right)\)
\(N_w = 1665.7\)
Since, the pan is excluded therefore number of particles per unit mass of particles 200-mesh or larger, so dividing the result by \((1-0.0075 = 0.9925)\) to exclude the pan.
\(N_w = \frac{1665.7}{0.9925} = 1679\) therefore, 1679 particles/g.
(b) volume mean diameter
using formula,
\( D_{v} = \left( \frac{1}{\sum_{i=1}^{n} \left( \frac{x_i}{{d_i}^3} \right)}\right)^{1/3} \)
\( D_{v} = \left(\frac{1}{8.8284} \right)^{1/3} = 0.4238 mm \)
(c) Volume-Surface Mean diameter
using formula,
\( D_{vs} = \frac{1}{\sum_{i=1}^{n} \left( \frac{x_i}{d_i} \right)} \)
\( D_{vs} = \frac{1}{0.828} = 1.207 mm \)
(d) Mass Mean Diameter
using formula,
\( D_{w} = \sum_{i=1}^{n} {x_i}{d_i} = 1.677\)
Thus, for the given screening data we have calculated the average diameters.
Online Excel Calculator for Average Particle Size
User can change the values present in yellow column and the calculations are performed as per formula mentioned in this article.
Resources:
- “Unit Operations in Chemical Engineering” (McCabe et al.)
- “Particle Technology and Separation Processes” (Richardson et al.)
- “Chemical Engineering Design: Principles, Practice and Economics of Plant and Process Design” (Towler and Sinnott)
Disclaimer: The Solver provided here is for educational purposes. While efforts ensure accuracy, results may not always reflect real-world scenarios. Verify results with other sources and consult professionals for critical applications. Contact us for any suggestions or corrections
