Table of Contents
The Arrhenius Equation is a fundamental formula used in reaction engineering to describe how the rate of a chemical reaction depends on temperature and the presence of an activation energy barrier. It was proposed by Svante Arrhenius in 1889.
The Arrhenius equation is given by:
\[k = A e^{-\frac{E_a}{RT}}\]
Where:
- \( k\) is the rate constant, units may vary depends upon the order of the reaction, for first-order reaction, it’s \( \text{s}^{-1} \)
- \( A \) is the pre-exponential factor, units for the pre-exponential factor are the same as those for the rate constant \( k \)
- \( E_a \) is the activation energy, measured in joules per mole (J/mol) or kilojoules per mole (kJ/mol).
- \( R \) is the universal gas constant, units are \( \text{J} \cdot \text{mol}^{-1} \cdot \text{K}^{-1} \) (joules per mole per kelvin).
- \( T \)is the absolute temperature, measured in kelvin (K)
Related: Performance Equation for Ideal Batch Reactor
Related: Arrhenius Activation Energy Calculator for two temperatures
Arrhenius Equation Calculator
The Calculator is useful in chemical kinetics for understanding how reaction rates change with varying conditions. The rate constant (k), activation energy (Ea), frequency factor (A), or temperature (T) are filled based on user input and calculation are performed using the Arrhenius equation. Value of R is used by default as 8.314 J/(mol*K).
Note: To show the units of k, we assumed first order reaction. However calculation are same for other rates of reactions as well.
Related: Heat Transfer through Conduction Calculator
Related: Performance Equation for Mixed Flow Reactor
What is Activation Energy
Activation energy (\( E_a \)) is described as the minimum amount of energy required for a chemical reaction to occur. It is defined as the energy needed to activate atoms or molecules to a state where they can undergo a chemical transformation or physical transport. In other words, it’s the energy barrier that reactants must overcome for a reaction to proceed.
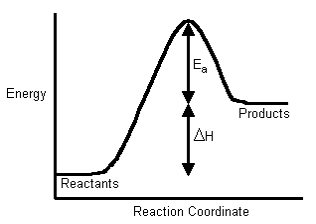
The equation for activation energy can be derived from the Arrhenius equation \(k = A \cdot e^{\frac{-E_a}{RT}}\)
Take the natural logarithm of both sides
\[\ln(k) = \ln(A) – \frac{E_a}{RT}\]
Isolate the activation energy (\(E_a\))
\[E_a = -R \cdot T \cdot \ln\left(\frac{k}{A}\right)\]
Example Problem based on Arrhenius Equation
The rate constant for the first order decomposition of \( \mathrm{H_2O_2} \) is given by the following equation:
\[\log k = 14.34 – \frac{1.25 \times 10^4 \, \text{K}}{T}\] Calculate \( E_a \) for this reaction and at what temperature will its half-period be 256 minutes?
The given expression for the rate constant is as follows:
\(\log k = 14.34 – \frac{1.25 \times 10^4 \, \text{K}}{T} \) \( \text{…(i)}\)
Comparing it with the Arrhenius equation, we get:
\(\log k = \log A – \frac{E_a}{2.303RT}\)
Therefore, \(\frac{E_a}{2.303R} = 1.25 \times 10^4\)
we get, activation energy is:
\(E_a = 239339 \, \text{J/mol} \)
\(E_a = 239.339 \, \text{kJ/mol}\)
The half-life period ( t_{1/2} ) is given as 256 minutes:
\(t_{1/2} = 256 \, \text{min} \)
\(= 256 \times 60 \, \text{sec}\)
The rate constant ( k ) can be calculated using the half-life formula for a first-order reaction:
\(k = \frac{0.693}{t_{1/2}}\)
\(k = \frac{0.693}{256 \times 60 \, \text{sec}}\)
\(k = 4.51 \times 10^{-5} \, \text{s}^{-1}\)
Substitute ( k ) in equation (i), we get:
\(\log (4.51 \times 10^{-5}) = 14.34 – \frac{1.25 \times 10^4 \, \text{K}}{T}\)
\(-4.35 = 14.34 – \frac{1.25 \times 10^4 \, \text{K}}{T}\)
\(T = \frac{1.25 \times 10^4 \, \text{K}}{18.69}\)
\(T = 669 \, \text{K}\)
Hence, the temperature at which the half-life period is 256 minutes is 669 K.
Python code Arrhenius Equation Calculation
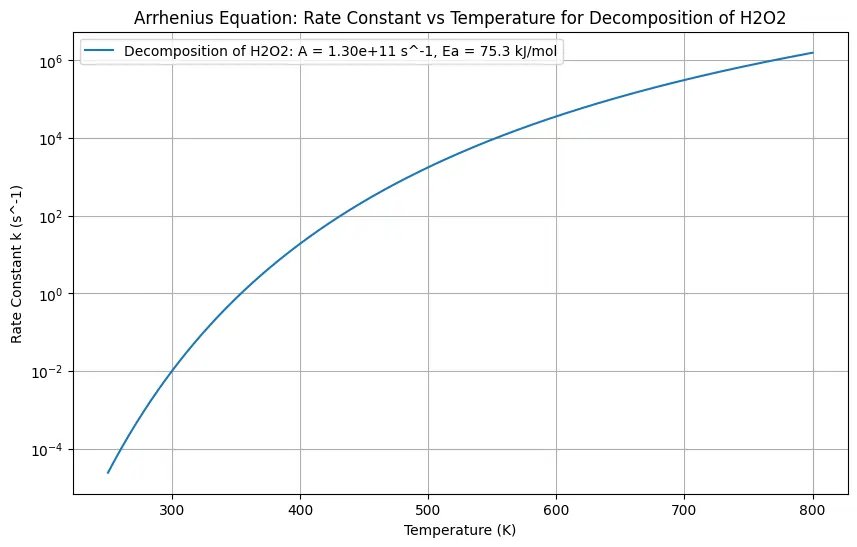
This python code is helpful for calculating the rate constants for the decomposition of hydrogen peroxide using the Arrhenius equation. The rate constants are plotted against a range of temperatures to visualize how the rate of decomposition varies with temperature.
Note: This Python code solves the specified problem. Users can copy the code and run it in a suitable Python environment. By adjusting the input parameters, users can observe how the output changes accordingly.
import numpy as np
import matplotlib.pyplot as plt
# Arrhenius equation function
def arrhenius_equation(A, Ea, T):
R = 8.314 # universal gas constant in J/(mol K)
return A * np.exp(-Ea / (R * T))
# Parameters for the decomposition of hydrogen peroxide
A = 1.3e11 # pre-exponential factor in s^-1
Ea = 75.3e3 # activation energy in J/mol
# Temperature range (in Kelvin)
T = np.linspace(250, 800, 500)
# Calculate rate constants
k = arrhenius_equation(A, Ea, T)
# Plotting
plt.figure(figsize=(10, 6))
plt.plot(T, k, label=f'Decomposition of H2O2: A = {A:.2e} s^-1, Ea = {Ea/1000} kJ/mol')
plt.xlabel('Temperature (K)')
plt.ylabel('Rate Constant k (s^-1)')
plt.title('Arrhenius Equation: Rate Constant vs Temperature for Decomposition of H2O2')
plt.legend()
plt.grid(True)
plt.yscale('log') # Logarithmic scale for better visualization
plt.show()Output:
Resources:
- Chemical Reactor Analysis and Design Fundamentals by Rawlings and Ekerdt
- Elements of Chemical Reaction Engineering by Fogler
- “Chemical Reaction Engineering“ by Octave Levenspiel
Disclaimer: The Solver provided here is for educational purposes. While efforts ensure accuracy, results may not always reflect real-world scenarios. Verify results with other sources and consult professionals for critical applications. Contact us for any suggestions or corrections.