Antoine Equation Calculator for Vapour Pressure versus Temperature Calculations

What is Antoine Equation?

The Antoine equation is a mathematical expression (empirical correlation) used to describe the non-linear thermodynamic relationship between the vapour pressure of a pure substance and its temperature. This equation is derived from Clausius Clapeyron Equation.

To find the vapour pressure of liquids and some solids over a range of temperatures. The equation is given by:

\[\log_{10}(P) = A – \frac{B}{C + T}\]

where:

• \(P\) is the vapor pressure.
• \(T\) is the temperature.
• \(A\), \(B\), and \(C\) are substance-specific constants.

The constants \(A\), \(B\), and \(C\) are determined empirically and are different for each substance.

Related: Joule-Thomson Effect – Coefficient Calculation for CO2 and N2

Antoine Equation Calculator for Vapour Pressure

This vapor pressure calculator uses the Antoine equation to calculate the vapor pressure of various chemicals (given in dropdown menu) with predefined Antoine coefficients (A, B, C) and temperature (in degrees Celsius), the calculator displays the vapor pressure in mmHg.

Related: Hydraulic Diameter Calculator for Circular and Non-Circular cross-section

Related: Inverse Square Law for Radiation

Antoine Equation Coefficients for pure compounds

Here we have provided the Coefficient of Antoine Equation for Pure compounds which are mostly used. Compounds are arranged in the alphabetical order. The Antoine Coefficient should only be used within the given temperature range T_min and T_max.

Data source: Hydrocarbon Processing, 68(10), p65-68, 1989. (Yaws, C. L. and Yang, H. C.)

Formula	Compound Name	A	B	C	TMIN (deg C)	TMAX (deg C)
C3H6O	acetone	7.2316	1277.03	237.23	-32	77
C2H4O2	acetic-acid	7.2996	1479.02	216.82	17	157
C2H3N	acetonitrile	7.0735	1279.2	224.01	-13	117
C6H6	benzene	6.90565	1211.033	220.79	-16	104
C4H10	butane	6.80896	935.86	238.73	-78	19
CCL4	carbon-tetrachloride	6.8941	1219.58	227.17	-20	101
C6H5Cl	chlorobenzene	6.9781	1431.05	217.56	47	147
C4H9Cl	1-chlorobutane	6.9379	1227.43	224.11	-18	112
C4H9Cl	2-chlorobutane	6.9447	1195.8	226.01	-23	102
CHCL3	chloroform	6.9371	1171.2	227	-13	97
C6H12	cyclohexane	6.8413	1201.531	222.647	6	105
C5H10	cyclopentane	6.88676	1124.162	231.361	-40	72
C10H22	decane	6.96375	1508.75	195.374	58	203
CH2Cl2	dichloromethane	7.0803	1138.91	231.46	-44	59
C4H10O	ethyl-ether	6.92032	1064.07	228.8	-61	20
C4H8O2	p-dioxane	7.0063	1288.5	211.01	2	137
C20H42	eicosane	7.1522	2032.7	132.1	198	379
C2H6O	Ethyl-alcohol (ethanol)	8.2133	1652.05	231.48	-3	96
C8H10	ethylbenzene	6.95719	1424.255	213.206	26	163
C2H6O2	ethylene-glycol	8.7945	2615.4	244.91	91	221
C7H16	heptane	6.89385	1264.37	216.636	-2	123
C6H14	hexane	6.87024	1168.72	224.21	-25	92
CH4O	methanol	8.0724	1574.99	238.87	-16	91
C4H8O2	ethyl-acetate	7.0146	1211.9	216.01	-13	112
CH3NO2	nitromethane	7.044	1291	209.01	5	136
C9H20	nonane	6.9344	1429.46	201.82	39	179
C8H18	octane	6.9094	1349.82	209.385	19	152
C5H12	pentane	6.87632	1075.78	233.205	-50	58
C6H6O	phenol	7.1345	1516.07	174.57	72	208
H20	Water (liquid)	8.07131	1730.63	233.426	1	100
H20	Water (vapour)	8.14019	1810.94	244.485	99	374

Example Problem on Antoine Equation

Given the Antoine equation for benzene, \[\log_{10} P_{\text{sat}} = 6.90 – \frac{1211}{220.8 + T}\] where \(P_{\text{sat}}\) is the saturation pressure in torr and (T) is the temperature in °C, estimate the heat of vaporization of benzene at \(60^\circ\text{C}\).

Given equation is the generalised form of Antoine Equation which can be interpreted to calculate the values of \(P_{sat}\), we get the following table on calculation (assuming heat of vaporization \( \Delta H_{\text{vap}} \) is constant in this narrow region of 60 °C).

Temp \((^\circ\text{C})\)	\(P_{sat}\)	\(ln_{P_{sat}}\)	\(\frac{1}{T}\) (1/K)
55	322.9513139	5.777501581	0.00304878
65	460.0141266	6.131257199	0.00295858

using the Clausius-Clapeyron equation,

Related: Read out our full article on Clausius-Clapeyron equation.

\[\ln P_{\text{sat}} = -\frac{\Delta H_{\text{vap}}}{R} \left(\frac{1}{T}\right) + C\]

here,

• \( P_{\text{sat}} \) is the saturation pressure,
• \( \Delta H_{\text{vap}} \) is the enthalpy of vaporization,
• \( R \) is the universal gas constant,
• \( T \) is the temperature in Kelvin,
• \( C \) is a constant of integration.

The plot for the values of \(\ln P_{\text{sat}}\) vs \(\frac{1}{T}\) is plotted below and slope of this line is calculated, based on the given slope value, \( \Delta H_{\text{vap}} \) is calculated.

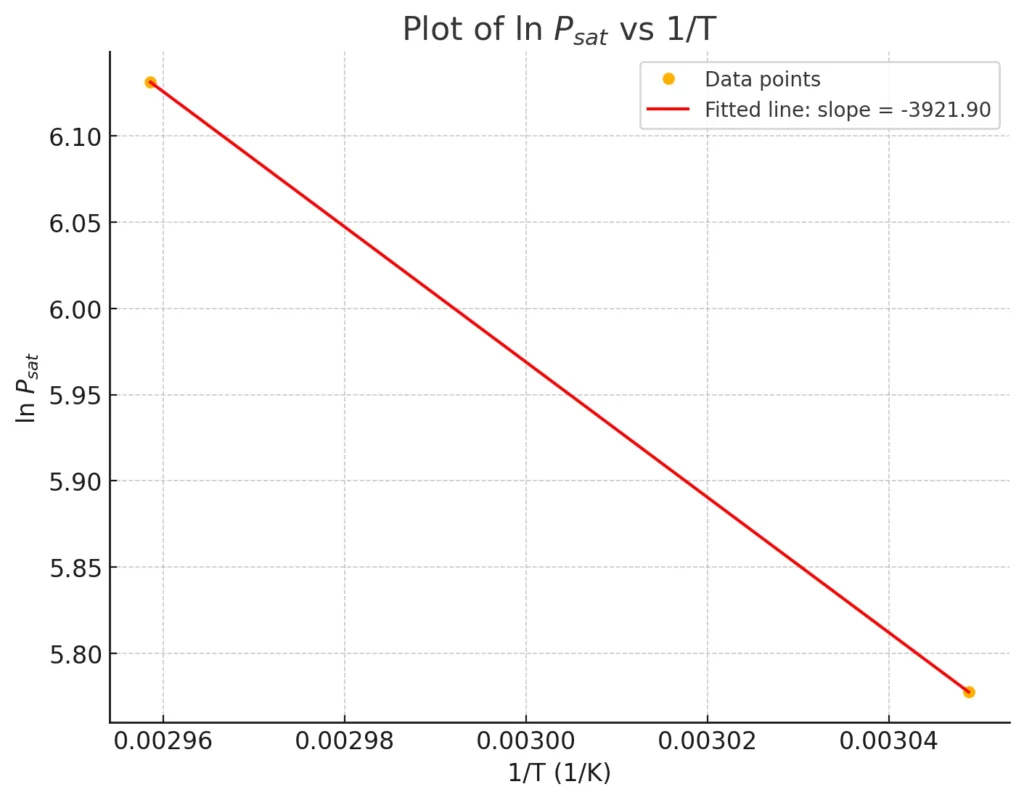
we get, the slope value from plot is -3921.90

therefore, the value of \(-\frac{\Delta H_{\text{vap}}}{R} = -3921.90\)

on calculation, \(\Delta H_{\text{vap}} = 32606.4\) J/mol which is equal to 32.6 KJ/mol.

The heat of vaporization of benzene at \(60^\circ\text{C}\) is 32.6 KJ/mol.

Related: Van der Waals Equation Calculator and PV Isotherm for Real Gases

Also Read: Kirchoff’s Law of Thermal Radiation, Wien’s Displacement Law

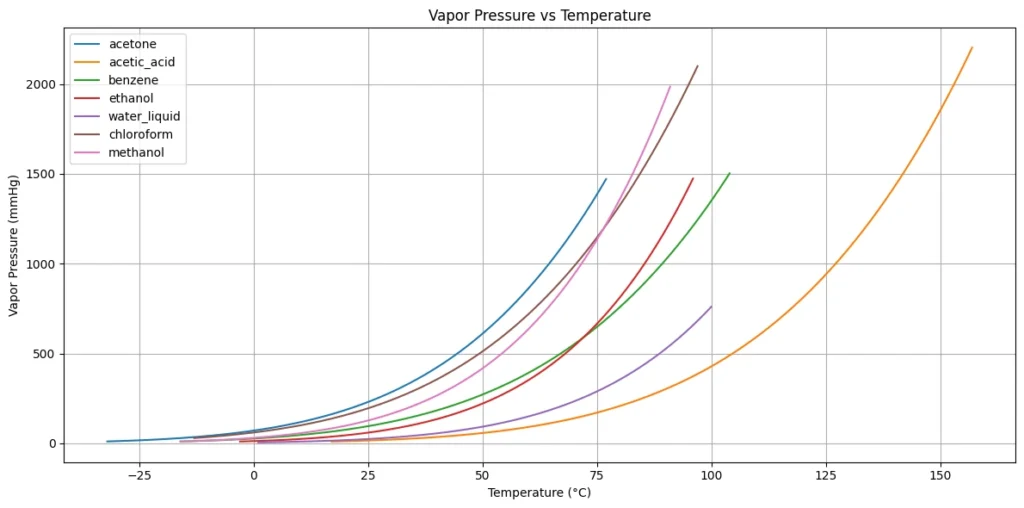
Python Code for Vapor Pressure Calculation

This python code helps user to calculate the Vapor Pressure using Antoine Equation versus temperature based on coefficients A, B, and C specific to each chemical, which are provided in the chemicals_data dictionary for the given temperature range.

Note: This Python code solves the specified problem. Users can copy the code and run it in a suitable Python environment. By adjusting the input parameters, users can observe how the output changes accordingly.

import numpy as np
import matplotlib.pyplot as plt

# Function to calculate vapor pressure using Antoine equation
def antoine_equation(A, B, C, T):
    return 10**(A - (B / (C + T)))

# Data for chemicals (A, B, C from Antoine equation)
chemicals_data = {
    'acetone': {'A': 7.2316, 'B': 1277.03, 'C': 237.23, 'temp_range': (-32, 77)},
    'acetic_acid': {'A': 7.2996, 'B': 1479.02, 'C': 216.82, 'temp_range': (17, 157)},
    'benzene': {'A': 6.90565, 'B': 1211.033, 'C': 220.79, 'temp_range': (-16, 104)},
    'ethanol': {'A': 8.2133, 'B': 1652.05, 'C': 231.48, 'temp_range': (-3, 96)},
    'water_liquid': {'A': 8.07131, 'B': 1730.63, 'C': 233.426, 'temp_range': (1, 100)},
    'chloroform': {'A': 6.9371, 'B': 1171.2, 'C': 227, 'temp_range': (-13, 97)},
    'methanol': {'A': 8.0724, 'B': 1574.99, 'C': 238.87, 'temp_range': (-16, 91)}
}

# Plotting vapor pressure versus temperature for each chemical
plt.figure(figsize=(12, 6))
for chemical, data in chemicals_data.items():
    A = data['A']
    B = data['B']
    C = data['C']
    temp_min, temp_max = data['temp_range']
    
    # Create temperature range within the specified range for each chemical
    temperature_range = np.linspace(temp_min, temp_max, 500)
    
    # Calculate vapor pressure
    vapor_pressure = antoine_equation(A, B, C, temperature_range)
    
    # Plot vapor pressure versus temperature
    plt.plot(temperature_range, vapor_pressure, label=chemical)

plt.title('Vapor Pressure vs Temperature')
plt.xlabel('Temperature (°C)')
plt.ylabel('Vapor Pressure (mmHg)')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()

Output:

Antoine Equation Excel Calculator

You can use this Excel data sheet for quick calculations. Enter the temperature in the designated orange cell and select the chemical of your choice. To simplify the process, we have listed approximately 700 chemicals. When a chemical is selected, the corresponding A, B, and C coefficients will be automatically retrieved, and the applicable temperature range for that chemical will be displayed. The vapor pressure at the given temperature will then be calculated using the Antoine Equation.

Resources

• “Thermodynamics: An Engineering Approach” by Yunus A. Çengel and Michael A. Boles
• LIBRARY OF PHYSICO-CHEMICAL PROPERTY DATA – Data Source Link
• “Introduction to Chemical Engineering Thermodynamics” by J.M. Smith, H.C. Van Ness, and M.M. Abbott
• NPTEL Lectures on Thermodynamics
• Antoine Coefficient Data source
• Antoine equation coefficients published in the NIST Chemistry WebBook for a variety of common chemicals

Disclaimer: The Solver provided here is for educational purposes. While efforts ensure accuracy, results may not always reflect real-world scenarios. Verify results with other sources and consult professionals for critical applications. Contact us for any suggestions or corrections.