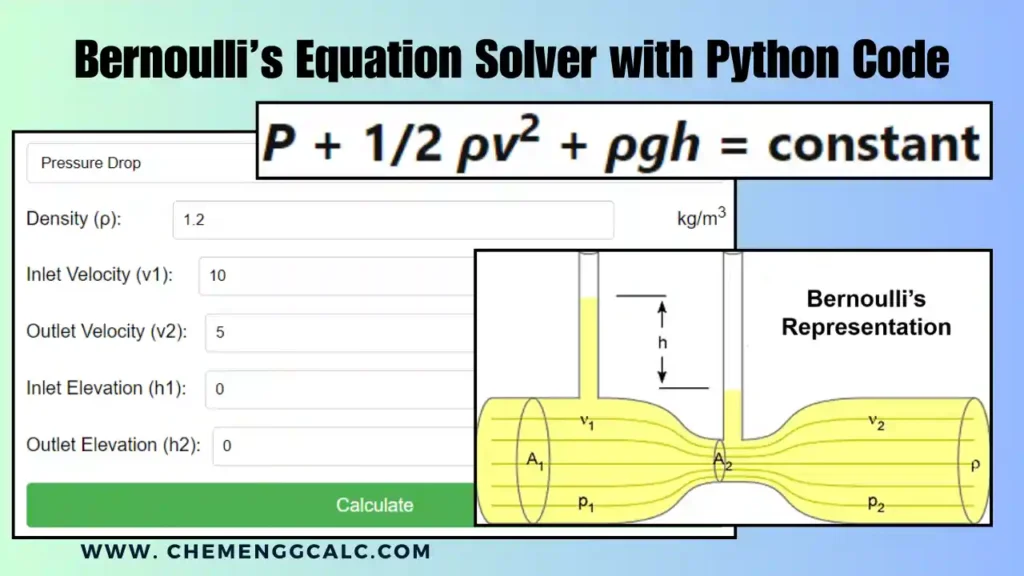
Have you ever noticed how honey flows slowly compared to water? That’s because of a property of fluids called viscosity, which describes their resistance to flow. Newton’s law of viscosity describes the relationship between a fluid’s resistance to flow (viscosity) and the shear stress applied to it.
Newton’s Law of Viscosity Calculator
This Viscosity Calculator works in four modes – Solve Newton’s law of viscosity directly for shear stress, viscosity, or shear rate. Find shear rate from plate velocity and gap width. Find shear stress from force and area. Or convert between dynamic and kinematic viscosity
Both Newtonian and non-Newtonian fluids are supported. The chart plots shear stress against shear rate with your operating point marked where a straight line for a Newtonian fluid, where the slope is the viscosity, and a curve under the power-law model for shear-thinning or shear-thickening behaviour.
Related: Friction Factor Calculator Moody’s Diagram for Smooth and Rough Pipes
Related: Head Loss or Pressure Loss Calculator using Darcy-Weisbach Equation
We have created a video for our viewers it explains the viscosity and why Newtonian and non-Newtonian fluids behave differently under shear.
Newton’s Law of Viscosity
Newton’s Law of Viscosity states that the shear stress \(\tau\) experienced by a fluid is directly proportional to the velocity gradient, or shear rate du/dy, within the fluid. Such fluids which obeys this law are known as Newtonian Fluids.
In mathematical terms, newton’s law of viscosity is expressed as:
\[ \tau =\frac{F}{A} = \mu \frac{du}{dy} \]
where,
- \(\tau\) is the shear stress (measured in units of force per unit area)
- \(\mu\) is the Dynamic viscosity of the fluid (measured in units of Pascal-seconds or poise)
- \(\frac{du}{dy}\) is the shear rate (represents the rate of change of velocity with respect to distance perpendicular to the direction of flow)
Related: Ergun Equation Calculator for Pressure Drop in Packed Bed Column
Related: Hagen-Poiseuille Equation Calculator / Poiseuille’s Law Solver
Newtonian vs Non-Newtonian Fluids
Newton’s law assumes viscosity is a constant: double the shear rate and the shear stress doubles with it. Fluids that behave this way are called Newtonian — water, air, most gases, light oils, glycerin and honey all qualify.
On a shear stress versus shear rate plot they trace a straight line through the origin, and its slope is the viscosity.
Many industrially important fluids do not. For these non-Newtonian fluids, viscosity itself changes with how hard the fluid is being sheared, so quoting a single viscosity value is meaningless without also stating the shear rate.
The power-law (Ostwald–de Waele) model
The most widely used description is the power law: τ = K (du/dy)ⁿ
where K is the consistency index (Pa·sⁿ) and n is the dimensionless flow behaviour index. The apparent viscosity (μapp) at any shear rate follows from it:
μapp = τ / (du/dy) = K (du/dy)ⁿ⁻¹
- n < 1 — shear-thinning (pseudoplastic). Apparent viscosity falls as shear rate rises. Ketchup, blood, paint, polymer melts and most slurries. This is by far the commonest case.
- n = 1 — Newtonian. The power law collapses back to Newton’s law, with K equal to μ.
- n > 1 — shear-thickening (dilatant). Apparent viscosity rises with shear rate. Concentrated cornflour suspensions and some ceramic slurries.
The table below shows the typical values of n and the flow behavior for various materials.
| Fluid | n | Behaviour |
|---|---|---|
| Ketchup | ≈ 0.27 | Strongly shear-thinning |
| Blood | ≈ 0.75 | Mildly shear-thinning |
| Polymer melts | 0.3 – 0.7 | Shear-thinning |
| Water, air, glycerin | 1.00 | Newtonian |
| Cornflour suspension | > 1 | Shear-thickening |
Terminologies Used in Newton’s Law of Viscosity
Shear stress
Imagine a fluid sandwiched between two plates. When one plate moves relative to the other, the fluid experiences a dragging force. This force per unit area acting parallel to the layers of the fluid is called shear stress.
Velocity gradient
As the plate moves, the fluid layers closer to it will move faster than the layers further away. This difference in velocity across the fluid is called the velocity gradient.
Assumption for Newton’s Law of Viscosity
- The fluid is assumed to be in a steady state with constant flow conditions
- Fluid being the homogeneous and isotropic, that means properties (such as viscosity) are uniform throughout and do not vary with direction
- No Slip Boundary Condition – The velocity at the boundary assumed to be zero
- This law is applicable to both laminar and turbulent flows, it’s often used for laminar flow conditions
Dynamic vs. Kinematic Viscosity
Dynamic viscosity reflects the internal friction a fluid experiences when external forces or stresses try to make it flow. Imagine honey – its high dynamic viscosity means it needs a strong force to overcome its internal friction and move easily. The SI unit for dynamic viscosity is Pascal-second (Pa·s), and it’s often represented by the symbol μ (mu).
Its formula relates shear stress (τ, tau) to the velocity gradient (du/dy) within the fluid: τ = μ * (du/dy).
Kinematic viscosity, focuses on a fluid’s internal resistance specifically under the influence of gravity. It essentially tells you how quickly a fluid can flow due to gravity acting on it. Think of how water flows much faster than oil – their kinematic viscosities differ significantly.
Kinematic viscosity \(v\) is calculated by dividing the dynamic viscosity \(\mu\) by the fluid’s density \(\rho\). This value is measured in square meters per second (m²/s).
\[v = \frac{\mu}{\rho}\]
Related: Reynolds Number Calculator for a Circular Pipe
Example Problem on Newton’s Law of Viscosity
An infinite plate is moved over a second plate on a layer of liquid as shown. For small gap width, d, we assume a linear velocity distribution in the liquid. The liquid viscosity is 0.65 centipoise and its specific gravity is 0.88. Given values, u = 0.3 m/s , distance across the plate (d) = 0.3mm Determine:
- (a) The absolute viscosity of the liquid, in lbf s/ft2.
- (b) The kinematic viscosity of the liquid, in m²/s.
- (c) The shear stress on the upper plate, in lbf/ft2.
- (d) The shear stress on the lower plate, in Pa.
- (e) The direction of each shear stress calculated in parts (c) and (d).
Given:
- Viscosity of liquid (\(\mu\)) = 0.65 centipoise
- Specific Gravity (\(SG\)) = 0.88
- velocity, \(u\) = 0.3 m/s
- distance across the plate, d = 0.3 mm = 0.0003 m
(a) The absolute viscosity of the liquid, in lbf s/ft2
converting centipoise into lbf s/ft2 , 1cp = 2.088 * 10-4 lbf s/ft2
\( \mu = 0.65 \, \text{cp} * 0.0000208854 \, \text{lbf s/ft}^2/\text{cp} \)
\(\mu = 1.36 * 10^{-5}\) \(\text{lbf s/ft}^2 \)
(b) The kinematic viscosity of the liquid, in m²/s.
First, we will calculate the density (\(\rho\)) of the liquid using the specific gravity (SG) and the density of water (\(ρ_w\))
\( \rho = \text{SG} * \rho_w = 0.88 * 62.4 \, \frac{lbf}{ft^3}\)
therefore, \(\rho = 54.912 \) \(\frac{lbf}{ft^3}\)
now, using formula Kinematic Viscosity = Dynamic Viscosity / Density
\( \nu = (\mu)/(\rho) = \frac{0.00043745 \, \text{lbf s/ft}^2}{54.912 \, \text{lbf/ft}^3}\)
\( \nu = 7.957 * 10^{-6} \, \text{ft}^2/\text{s} \) = \(7.39 * 10^{-7} \frac{m^2}{s}\)
(c) The shear stress on the upper plate, in lbf/ft2.
using the formula for newton’s law of viscosity, \( \tau = \mu \frac{du}{dy} \)
let’s first calculate the velocity gradient,
\(\frac{du}{dy} = \frac{0.3}{0.0003} s^{-1}\) = \(1000 s^{-1}\)
\(\tau_{upper} = 1.36 * 10^{-5} \text{lbf s/ft}^2 * 1000 s^{-1} \)
\(\tau_{upper} = 0.0136 \frac{lbf}{ft^2}\)
(d) The shear stress on the lower plate, in Pa.
by converting into Pascals, using conversion \(\frac{lbf}{ft^2}\ = 47.88 Pa\)
\(\tau_{lower} = 0.0136 * 47.88 = 0.65 Pa\)
(e) The direction of each shear stress calculated in parts (c) and (d).
The shear stress on the upper plate (part c) acts in the opposite direction i.e negative x direction to the motion of the upper plate, while the shear stress on the lower plate (part d) in the positive x direction acts in the same direction as the motion of the upper plate.
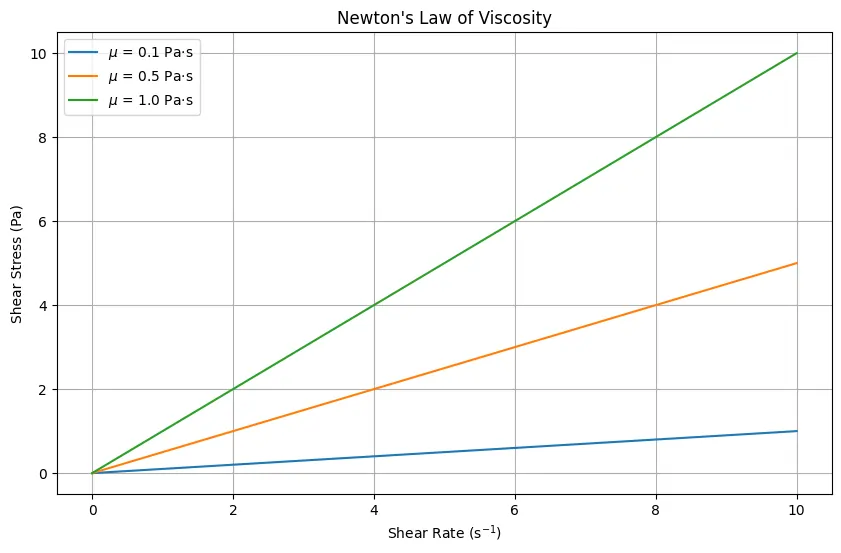
Python Code for Newton’s Law of Viscosity
This python code calculates the shear stress \(\tau\) using Newton’s law of viscosity \( \tau =\mu \frac{du}{dy} \) for a range of shear rates \(\frac{du}{dy}\) at different \(\mu\) values. Then, it plots the relationship between shear stress and shear rate . Adjust the values of mu and du_dy as needed.
Note: This Python code solves the specified problem. Users can copy the code and run it in a suitable Python environment. By adjusting the input parameters, users can observe how the output changes accordingly.
import numpy as np
import matplotlib.pyplot as plt
# Constants
mu_values = [0.1, 0.5, 1.0] # Dynamic viscosity (Pa·s) - Three different values
du_dy = np.linspace(0, 10, 100) # Shear rate (s^-1)
# Plotting
plt.figure(figsize=(8, 6))
for mu in mu_values:
# Calculate shear stress using Newton's law of viscosity
tau = mu * du_dy
# Plot shear stress vs. shear rate
plt.plot(du_dy, tau, label=f'$\mu$ = {mu} Pa·s')
plt.xlabel('Shear Rate (s$^{-1}$)')
plt.ylabel('Shear Stress (Pa)')
plt.title("Newton's Law of Viscosity")
plt.grid(True)
plt.legend()
plt.show()Output:
Resources:
- “Introduction to Fluid Mechanics and Fluid Machines” by Y. M. Joshi
- “Transport Phenomena” by Bird, Stewart, and Lightfoot.
- “Introduction to Chemical Engineering Fluid Mechanics” by William M. Deen.
- “Fluid Mechanics” by Frank M. White.
Disclaimer: The Solver provided here is for educational purposes. While efforts ensure accuracy, results may not always reflect real-world scenarios. Verify results with other sources and consult professionals for critical applications. Contact us for any suggestions or corrections.
