Weber Number Calculator

What is Weber Number?

The Weber number (We) is a dimensionless number in fluid mechanics, which is used to describe the relative importance of the inertial forces to the surface tension forces in a fluid flow. It is used in the study of multiphase flows, such as the behavior of droplets, bubbles, and jets.

Weber Number (We) is defined as,

\[\text{We} = \frac{\text{Inertial Force}}{\text{Surface Tension Force}}\]

\[\text{We} = \frac{ \rho u^2 L^2}{\sigma L}= \frac{ \rho u^2 L}{\sigma}\]

where,

\(\rho\) is the fluid density,
\(u\) is the characteristic velocity of the fluid,
\(L\) is the characteristic length (usually the diameter of a droplet or bubble),
\(\sigma\) is the surface tension of the fluid

This calculator helps user to compute the \((\text{We})\) number based on the user input values for fluid density \((\rho)\), characteristic velocity \((u)\), characteristic length \((L)\), and surface tension \((\sigma)\). This number provides insights into fluid behavior, especially concerning droplets, bubbles, and other fluid structures influenced by surface tension and flow dynamics.

Interactive Weber Number Calculator

Weber Number Significance

The Weber number is useful in understanding thin film flows, droplet formation, and bubble dynamics. It indicates whether kinetic or surface tension energy prevails in a given flow

Case 1 – Low Weber Number (We << 1)

Surface tension forces dominate over inertial forces, For example, Bubble slowly rising in the viscous liquid.

Case 2 – Medium Weber Number (We ~ 1)

Inertial forces and surface tension forces are of comparable magnitude. For example, Droplets falling through air with slight deformation.

Case 1 – High Weber Number (We >> 1)

Inertial forces dominate over surface tension forces. For example, splashing of water when brick hits on the surface

Consider a raindrop falling through the air.

Let’s assume:

Density of water \((\rho)\) = 1000 kg/m³,
Velocity of the raindrop \((v)\) = 5 m/s,
Diameter of the raindrop \((L)\) = 2 mm (0.002 m),
Surface tension of water \((\sigma)\) = 0.072 N/m.

The \(\text{We}\) for the falling raindrop can be calculated as:

\(\text{We} = \frac{\rho v^2 L}{\sigma} = \frac{1000 \times 5^2 \times 0.002}{0.072}\)

\( \text{We} = \frac{1000 \times 25 \times 0.002}{0.072} \approx 694.4\)

It suggests that inertial forces are much stronger than surface tension forces, meaning the raindrop is likely to deform or break apart as it falls through the air.

Another example, Consider a droplet of water falling from a tap. As the droplet detaches, the We number determines whether the droplet maintains its shape (low We, where surface tension dominates) or breaks up into smaller droplets (high We, where inertial forces dominate).

Other Dimensionless Numbers

Here we have tabulated the list of dimensionless numbers which are commonly used in Chemical Engineering with their formula, definition, and significance.

Dimensionless Number	Formula	Definition	Significance
Reynolds Number (Re)	\[\text{Re} = \frac{\rho u L}{\mu} = \frac{u L}{\nu}\]	Ratio of inertial forces to viscous forces.	Determines flow regime: Re < 2000: Laminar flow Re > 4000: Turbulent flow. Critical for pipe flow and reactors.
Prandtl Number (Pr)	\[\text{Pr} = \frac{C_p \mu}{k}\]	Ratio of momentum diffusivity to thermal diffusivity.	It indicates the relative thickness of momentum and thermal boundary layers in heat transfer.
Nusselt Number (Nu)	\[\text{Nu} = \frac{h L}{k}\]	Ratio of convective to conductive heat transfer.	It is used in convective heat transfer problems to evaluate heat transfer coefficients.
Sherwood Number (Sh)	\[\text{Sh} = \frac{k_m L}{D}\]	Ratio of convective to diffusive mass transfer.	It is important in mass transfer, especially in diffusion and absorption processes.
Péclet Number (Pe)	\[\text{Pe} = \text{Re} \cdot \text{Pr}\]	Ratio of advection to diffusion. Combines Reynolds and Prandtl numbers.	It is important in heat and mass transfer processes where advection dominates over diffusion.
Schmidt Number (Sc)	\[\text{Sc} = \frac{\mu}{\rho D}\]	Ratio of momentum diffusivity to mass diffusivity.	It is used in mass transfer to relate momentum and mass transport. Analogous to the Prandtl number in heat transfer.
Lewis Number (Le)	\[\text{Le} = \frac{\alpha}{D} = \frac{\text{Sc}}{\text{Pr}}\]	Ratio of thermal diffusivity to mass diffusivity.	It relates thermal and mass transport; Le = 1 implies similar thermal and mass diffusivity.
Fourier Number (Fo)	\[\text{Fo} = \frac{\alpha t}{L^2}\]	Ratio of heat conduction rate to heat storage rate.	It is used in unsteady-state heat transfer problems, like transient conduction.
Biot Number (Bi)	\[\text{Bi} = \frac{h L}{k}\]	Ratio of internal thermal resistance to surface thermal resistance.	It determines whether heat conduction is lumped or distributed. Bi < 0.1: Lumped system approximation valid.
Weber Number (We)	\[\text{We} = \frac{\rho u^2 L}{\sigma}\]	Ratio of inertial forces to surface tension forces.	It is important in multiphase flows, droplet formation, and fluid interface stability.
Capillary Number (Ca)	\[\text{Ca} = \frac{\mu u}{\sigma}\]	Ratio of viscous forces to surface tension forces.	It is used to study the behavior of capillary flows and thin-film phenomena.
Froude Number (Fr)	\[\text{Fr} = \frac{u^2}{g L}\]	Ratio of inertial forces to gravitational forces.	It is important in free-surface flows, mixing, and fluidized bed design.
Damköhler Number (Da)	\[\text{Da} = \frac{\text{Reaction rate}}{\text{Flow rate}}\]	Ratio of chemical reaction time to residence time.	It is important in chemical reaction engineering; determines if a process is reaction- or transport-limited.
Thiele Modulus (ϕ)	\[\phi = L \sqrt{\frac{k}{D}}\]	Ratio of reaction rate to diffusion rate within a catalyst particle.	It is used in heterogeneous catalysis to determine diffusion limitations within catalyst pores.
Knudsen Number (Kn)	\[\text{Kn} = \frac{\lambda}{L}\]	Ratio of molecular mean free path to characteristic length.	It is important in gas flow through small pores or microchannels; indicates continuum vs. molecular flow regime.
Eckert Number (Ec)	\[\text{Ec} = \frac{u^2}{C_p \Delta T}\]	Ratio of kinetic energy to enthalpy difference.	It is used in high-speed flows and heat transfer problems involving viscous dissipation.
Grashof Number (Gr)	\[\text{Gr} = \frac{g \beta \Delta T L^3}{\nu^2}\]	Ratio of buoyancy forces to viscous forces.	It determines the importance of natural convection in heat transfer problems.
Stanton Number (St)	\[\text{St} = \frac{h}{\rho u C_p}\]	Ratio of heat transfer coefficient to the product of fluid velocity and specific heat.	It is used in heat transfer to describe convective heat transfer efficiency relative to bulk flow.

Table: Dimensionless Numbers

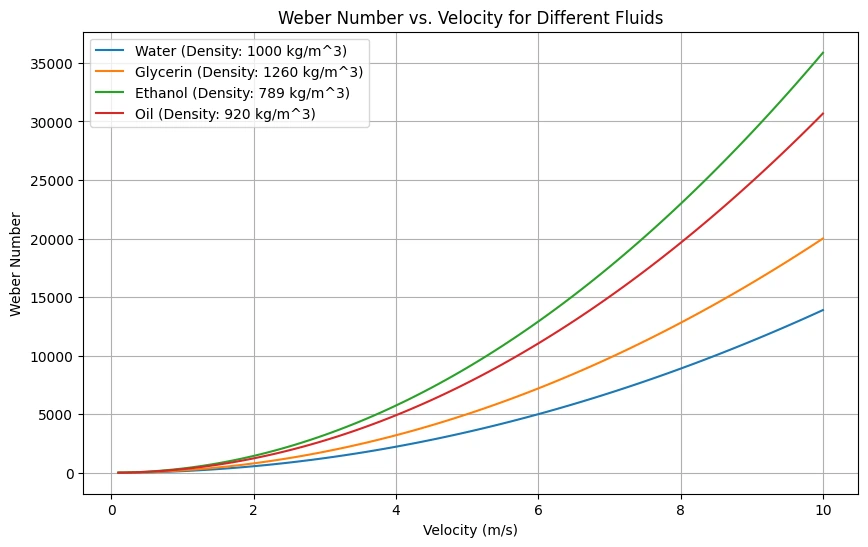
Python Code for Weber Number

This python code calculates and plots the Weber number for different fluids (water, glycerin, ethanol, and oil) as a function of velocity. This code is helpful in analysis of fluid flow for varying conditions.

Note: This Python code solves the specified problem. Users can copy the code and run it in a suitable Python environment. By adjusting the input parameters, and observe how the output changes accordingly.

import numpy as np
import matplotlib.pyplot as plt

def calculate_weber_number(density, velocity, length, surface_tension):
    return (density * velocity**2 * length) / surface_tension

# Constants
length = 0.01  # m (characteristic length)
surface_tension_water = 0.072  # N/m (for water)
surface_tension_glycerin = 0.063  # N/m (for glycerin)
surface_tension_ethanol = 0.022  # N/m (for ethanol)
surface_tension_oil = 0.030  # N/m (for oil)

# Fluid properties: (density, surface_tension)
fluids = {
    'Water': (1000, surface_tension_water),         # kg/m^3, N/m
    'Glycerin': (1260, surface_tension_glycerin),   # kg/m^3, N/m
    'Ethanol': (789, surface_tension_ethanol),      # kg/m^3, N/m
    'Oil': (920, surface_tension_oil)               # kg/m^3, N/m
}

# Velocity range
velocity_range = np.linspace(0.1, 10, 100)  # m/s

# Plotting
plt.figure(figsize=(10, 6))

for fluid, (density, surface_tension) in fluids.items():
    weber_numbers = [calculate_weber_number(density, v, length, surface_tension) for v in velocity_range]
    plt.plot(velocity_range, weber_numbers, label=f'{fluid} (Density: {density} kg/m^3)')

plt.xlabel('Velocity (m/s)')
plt.ylabel('Weber Number')
plt.title('Weber Number vs. Velocity for Different Fluids')
plt.legend()
plt.grid(True)
plt.show()

Output:

Weber Number vs. Velocity for Different Fluids

Resources

“Fluid Mechanics” by Frank M. White
“Introduction to Fluid Mechanics” by Robert W. Fox, Alan T. McDonald, and Philip J. Pritchard
“Principles of Heat and Mass Transfer” by Frank P. Incropera and David P. DeWitt
Python.org – The official Python website offers tutorials, documentation, and resources for learning Python.

Disclaimer: The Solver provided here is for educational purposes. While efforts ensure accuracy, results may not always reflect real-world scenarios. Verify results with other sources and consult professionals for critical applications. Contact us for any suggestions or corrections.

Weber Number Calculator – Significance and Calculation

Table of Contents

What is Weber Number?