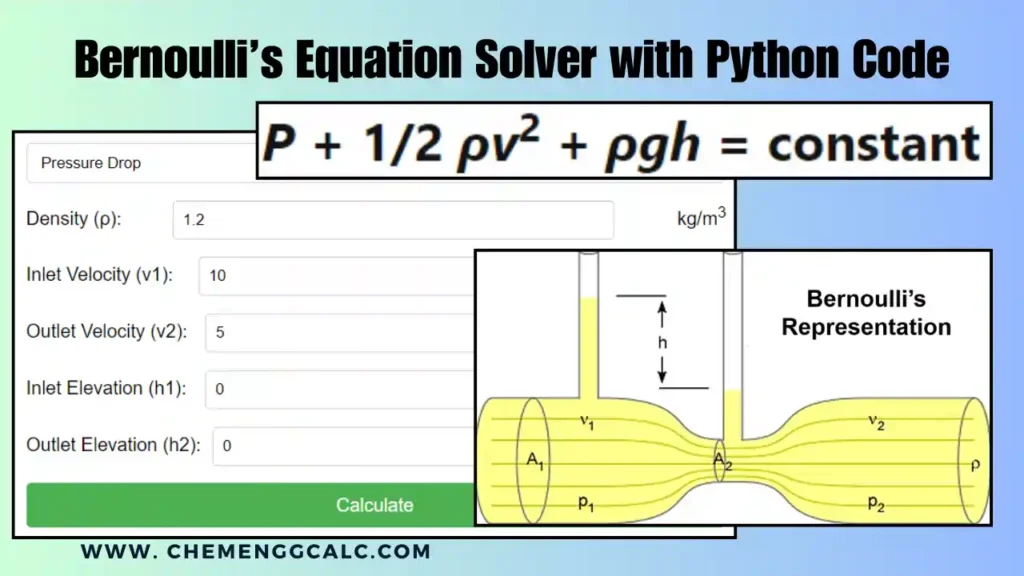
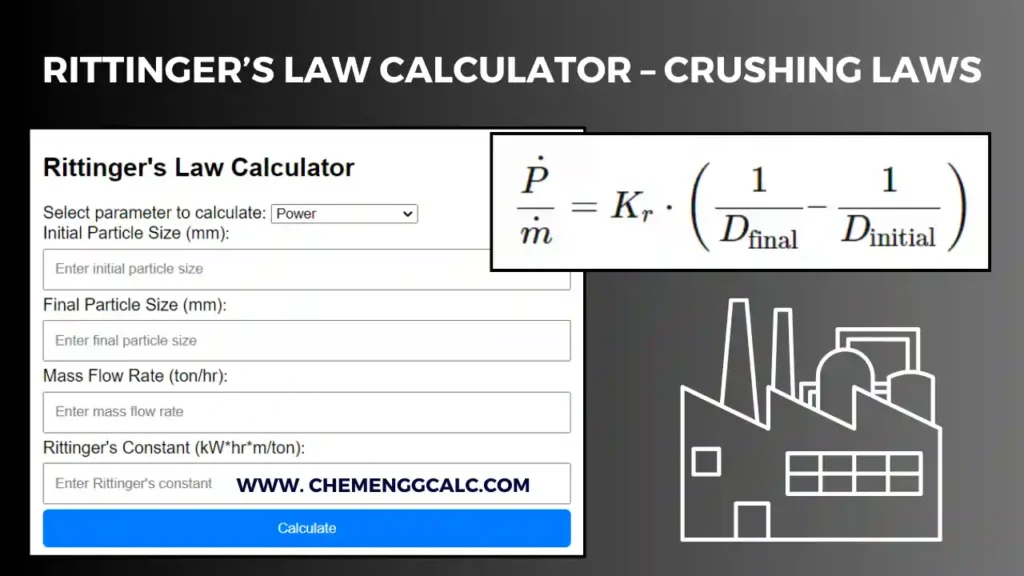
Table of Contents
Stokes’ Law is a fundamental principle in fluid dynamics that describes the motion of spherical objects through a viscous fluid. It is useful in many applications like sedimentation, aerosol, biology and other fields of chemical engineering.
What is Stoke’s Law
Stoke’s Law is an empirical relationship for the frictional force also called drag force exerted on spherical objects with very small Reynolds numbers in a viscous fluid. The law is derived considering the forces acting on a particular particle as it sinks through the liquid column under the influence of gravity.
Related: Reynolds Number Calculator for a Circular Pipe
Drag Force : The force that retards a sphere moving through a viscous fluid is directly proportional to the velocity and the radius of the sphere, and the fluid’s viscosity.
Mathematically, this can be expressed as:
\[F_{\text{d}} = 6\pi \mu Rv\]
where (in SI units):
- \(F_{\text{d}}\) is the frictional force – known as Stokes’ drag – acting on the interface between the fluid and the particle (newtons, kg m s\(^{-2}\));
- \(\mu\) (some author says, \(\eta\)) is the dynamic viscosity (Pascal-seconds, kg m\(^{-1}\) s\(^{-1}\));
- \(R\) is the radius of the spherical object (meters);
- \(v\) is the flow velocity relative to the object (meters per second).
Related: Heat and Mass Transfer – Analogy and Correlations for Chemical Engineers
Terminal Velocity Formula for Stoke’s Law
Terminal velocity is the constant velocity reached by an object falling through a fluid under the influence of gravity, where the gravitational force pulling the object downward is balanced by the drag force exerted by the fluid.
For objects falling through a fluid in a regime where Stokes’ law applies (i.e., for small spherical objects moving at low Reynolds numbers), the formula for terminal velocity can be derived from Stokes’ drag equation.
The terminal velocity (\(v_t\)) for Stokes’ law is given by:
\[v_t = \frac{{2R^2 (\rho_s – \rho_f)g}}{{9\eta}}\]
where (in SI unit)s:
- \(v_t\) is the terminal velocity (m/s),
- \(R\) is the radius of the falling object (m),
- \(\rho_s\) is the density of the object (kg/m\(^3\)),
- \(\rho_f\) is the density of the fluid (kg/m\(^3\)),
- \(g\) is the acceleration due to gravity (m/s\(^2\)),
- \(\eta\) is the dynamic viscosity of the fluid (Pa·s or kg/(m·s)).
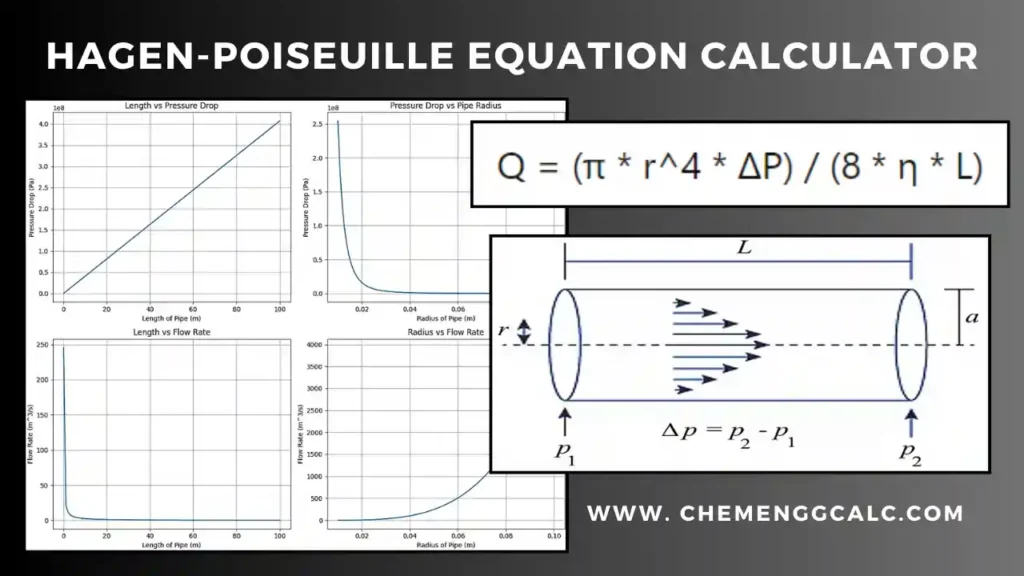
Stoke’s Law Calculator for Terminal velocity
This Stoke’s Law Calculator helps user to compute various parameters related to the motion of an object through a fluid under the influence of viscous drag, as described by Stokes’ law. Users can select parameters from a dropdown menu such as the terminal velocity of the object, the object’s radius, the density of the object or the fluid, the acceleration due to gravity, or the dynamic viscosity of the fluid. This calculator serves as a helpful tool for researchers, engineers, and students studying fluid dynamics and related fields.
Related: Newton’s Law of Viscosity Calculator
Related: Other Fluid Mechanics Calculator
Stoke’s Law Assumptions
Stokes’ law makes the following assumptions for the behavior of a particle in a fluid:
- Laminar flow – Imagine smooth, layered sheets of fluid moving around the object
- No inertial effects (zero Reynolds number) – The inertia of the fluid (its resistance to acceleration changes) is negligible compared to the viscous forces (forces due to the fluid’s internal friction).
- Spherical particles –
- Homogeneous (uniform in composition) material
- Smooth surfaces -A smooth surface minimizes friction between the object and the fluid.
- Particles do not interfere with each other – If particles are close together, they can influence each other’s drag forces.
Derivation for Terminal Velocity For a Sphere falling in a fluid
Consider a small spherical particle of mass (m) falling freely through a fluid of density (\(\rho_f\)) with the velocity (v) and achieves the terminal velocity with the given conditions. While flowing the particle experience various forces, let \(F_D\) be the drag force, \(F_B\) be the bouyant force, \(F_g\) be the gravitational force. At terminal velocity, \(v_t\) the net force of the object is zero.
Fig. Stoke’s Law representation (A Sphere free falling through a fluid)
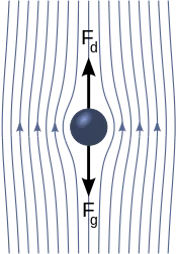
The upward forces are the buoyant force and the drag force.
The drag force on a small sphere moving through a viscous medium is given by:
\[F_{\text{D}} = 6\pi \eta rv\]
where:
- \(\eta\) is the dynamic viscosity of the fluid,
- r is the radius of the spherical object, and
- v is the velocity of the object.
The buoyant force is given by:
\[F_B = \frac{4}{3} \pi {r^3} {\rho_f} {g}\]
When the object is falling under the influence of gravity, the forces acting on it are the gravitational force (weight) i.e downward force. The gravitational force is given by:
\[F_g = \frac{4}{3} \pi {r^3} {\rho} {g}\]
where:
- g is the acceleration due to gravity,
- ρ is the density of the spherical object.
At terminal velocity, the net force on the object is zero, which means the sum of the forces acting on the object is zero. Therefore, we have:
\[F_g = F_D + F_B\]
\[\frac{4}{3} \pi {r^3} {\rho} {g} = 6\pi \eta rv\ + \frac{4}{3} \pi {r^3} {\rho_f} {g}\]
on, rearranging and solving above equation, we get
\[v_t = \frac{{2R^2 (\rho_s – \rho_f)g}}{{9\eta}}\]
This is the expression for the terminal velocity of a small spherical object moving through a viscous medium, according to Stoke’s Law. The terminal velocity is directly proportional to the square of the radius of the object, the difference in density between the object and the fluid, and inversely proportional to the viscosity of the fluid.
Please note that this derivation assumes that the object is small and moving slowly through the fluid, and that the flow of the fluid is laminar (not turbulent). If these conditions are not met, the actual terminal velocity may be different.
Also Read: Chemical Engineering as a career option in India
Example Problem on Stoke’s Law of Viscosity
In Millican’s oil drop experiment, what is the terminal velocity of an uncharged drop of radius \(2 \times 10^{-5}\) m and density \(1.2 \times 10^{3}\) kg/m\(^3\)? Take the viscosity of air at the temperature of the experiment to be \(1.8 \times 10^{-5}\) pas. How much is the viscous force on the drop at that speed? Neglect the buoyancy of the drop due to air.
Given:
- Radius, \(r\) = \(2 \times 10^{-5}\) m
- density, \(\rho_p\) = \(1.2 \times 10^{3}\) kg/m\(^3\)
- Viscosity of fluid (air), \(\eta\) = \(1.8 \times 10^{-5}\) pas
we know that from terminal velocity formula, Given that the buoyancy of the drop due to air is to be neglected.
\( v_T = \frac{{2r^2 g}}{{9 \eta}} \)
\( v_T = \frac{{2(2 \times 10^{-5})^2 \times 9.8}}{{9 \times 1.8 \times 10^{-5}}} \)
\( v_T = 5.81 \times {10^{-2}} \) m/s or 5.81 cm/s
To find the viscous force \(F\), we use
\( F = 6\pi \eta r v_T \)
F = 6π(1.8 × 10-5)(2 × 10-5)(5.81× 10-2)
Viscous force \(F\): \[ F = 3.94 \times 10^{-10}\, \text{N} \]
Related: 10 Mostly used Dimensionless Numbers in Chemical Engineering
Python Code for Stoke’s Law – Terminal Velocity Calculation
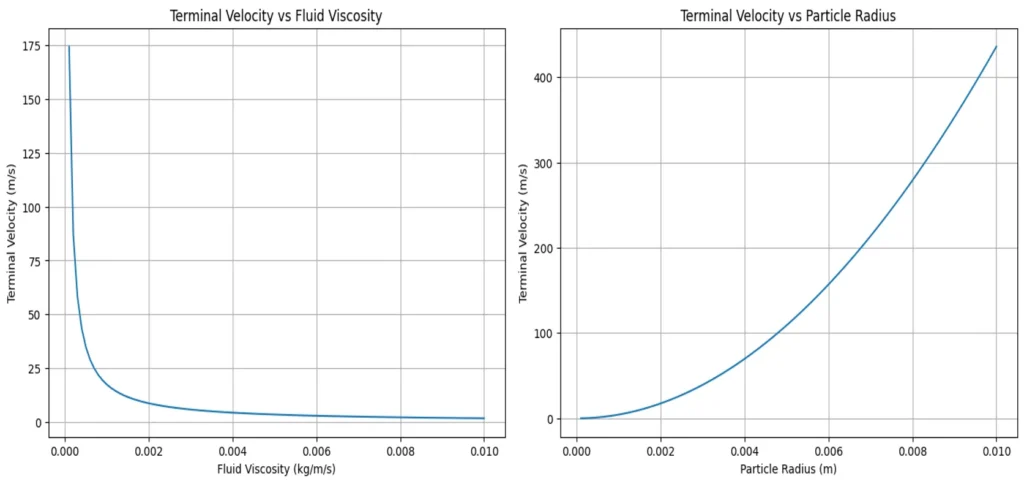
This python code helps user to understand how terminal velocity is changing with the change of radius and the change of fluid viscosity assuming the fluid density, particle density, gravity remains constant. This code calculates the terminal velocity of a particle suspended in a fluid according to Stokes’ law, which describes the drag force experienced by a small sphere moving through a viscous fluid at low Reynolds numbers.
Note: This Python code solves the specified problem. Users can copy the code and run it in a suitable Python environment. By adjusting the input parameters, users can observe how the output changes accordingly.
import numpy as np
import matplotlib.pyplot as plt
def stokes_terminal_velocity(radius, viscosity, density_particle, density_fluid):
g = 9.81 # acceleration due to gravity (m/s^2)
v_terminal = (2 * (radius ** 2) * (density_particle - density_fluid) * g) / (9 * viscosity)
return v_terminal
# Parameters
viscosity = 0.001 # viscosity of the fluid (kg/m/s)
density_particle = 2000 # density of the particle (kg/m^3)
density_fluid = 1.2 # density of the fluid (kg/m^3)
# Range of radius values
radii = np.linspace(0.0001, 0.01, 100) # m
# Calculate terminal velocities for different radii
terminal_velocities_radius = [stokes_terminal_velocity(radius, viscosity, density_particle, density_fluid) for radius in radii]
# Plot between radius and terminal velocity
plt.figure(figsize=(8, 6))
plt.plot(radii, terminal_velocities_radius)
plt.title("Terminal Velocity vs Particle Radius")
plt.xlabel("Particle Radius (m)")
plt.ylabel("Terminal Velocity (m/s)")
plt.grid(True)
plt.show()
# Range of viscosity values
viscosities = np.linspace(0.0001, 0.01, 100) # kg/m/s
# Calculate terminal velocities for different viscosities
terminal_velocities_viscosity = [stokes_terminal_velocity(radius, viscosity, density_particle, density_fluid) for viscosity in viscosities]
# Plot between viscosity and terminal velocity
plt.figure(figsize=(8, 6))
plt.plot(viscosities, terminal_velocities_viscosity)
plt.title("Terminal Velocity vs Fluid Viscosity")
plt.xlabel("Fluid Viscosity (kg/m/s)")
plt.ylabel("Terminal Velocity (m/s)")
plt.grid(True)
plt.show()Output:
Resources:
- “Unit Operations of Chemical Engineering” by Warren L. McCabe, Julian C. Smith, Peter Harriott
- “Fluid Mechanics” by Frank M. White
- “Fluid Mechanics: Fundamentals and Applications” by Çengel and Cimbala
Disclaimer: The Solver provided here is for educational purposes. While efforts ensure accuracy, results may not always reflect real-world scenarios. Verify results with other sources and consult professionals for critical applications. Contact us for any suggestions or corrections.