Table of Contents
Individual solid particles are characterized by their shape, size, and density. For regular shapes like cubes or spheres, it is easy to determine the particle shape. However, for irregular shapes (such as mica flakes or sand grains), the shape can be described using sphericity. The shape and sphericity of particles are important concepts in fields such as materials science, geology, and powder technology.
What is Sphericity?
Sphericity is a measure of how closely the shape of a particle resembles a sphere. It is defined as the ratio of the surface area of a sphere (with the same volume as the particle) to the surface area of the particle itself.
The formula for sphericity \((\Psi)\) is:
\[\Psi = \frac{\text{Surface area of sphere}}{\text{Surface area of the particle}}\]
Mathematically, it can be expressed as:
\[\Psi = \frac{\pi^{1/3} (6 V_p)^{2/3}}{A_p}\]
Where:
- \(V_p\) is the volume of the particle.
- \(A_p\) is the surface area of the particle.
Sphericity ranges varies from 0 to 1. A sphericity of 1 means the particle is a perfect sphere, A lower sphericity value shows a more irregular shape.
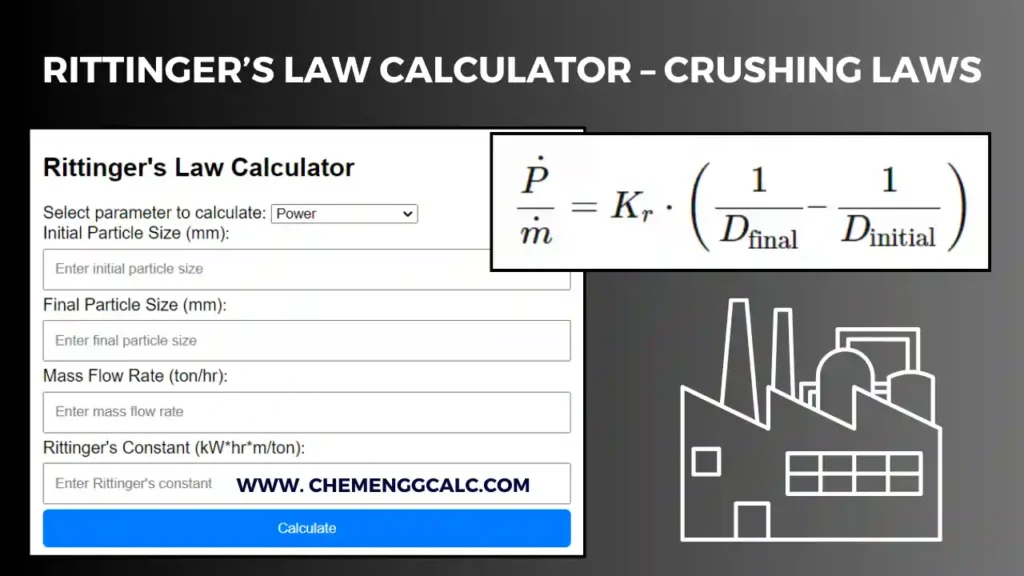
Related: Rittinger’s Law Calculator
Related: Kick’s Law Calculator
Sphericity Calculator
The sphericity calculator helps users determine the sphericity of various shapes, including cubes, cuboids, cylinders, spheres, and irregular shapes. The calculations are performed based on the volume and surface area of the shape. The tool ensures all input values are positive and within valid ranges.
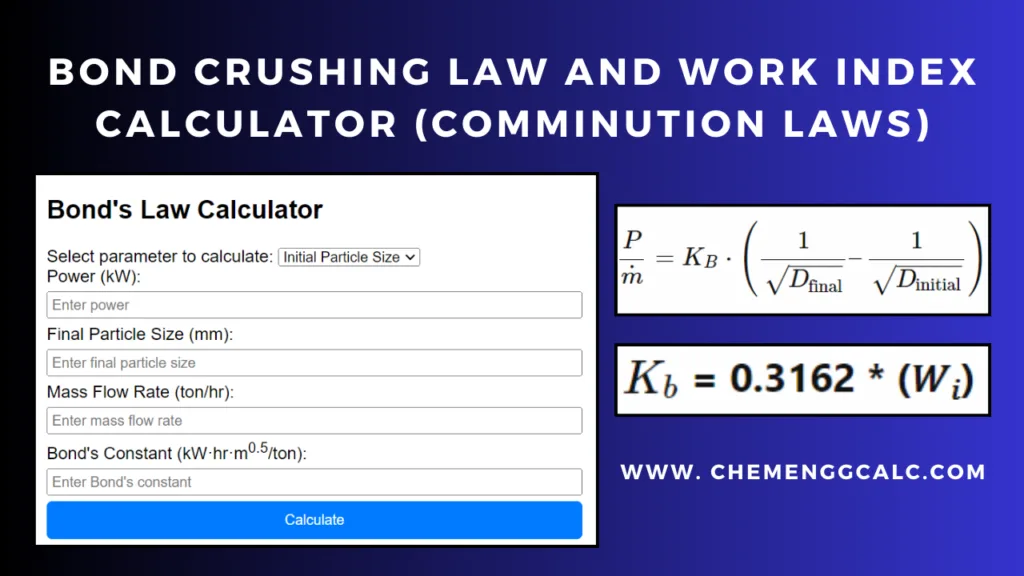
Related: Bond’s Law Calculator and Work Index
Sphericity Formula for Sphere
For perfect Sphere, the sphericity formula is Surface area of sphere divided by surface area of Sphere, which is equivalent to 1.
\[\Psi = \frac{\pi^{1/3} (V_{\text{sphere}})^{2/3}}{A_{\text{sphere}}}\]
Substituting the volume and surface area of the sphere:
\[\Psi = \frac{\pi^{1/3} \left( \frac{4}{3} \pi r^3 \right)^{2/3}}{4 \pi r^2} = 1\]
A sphere is the shape with the maximum sphericity of 1.
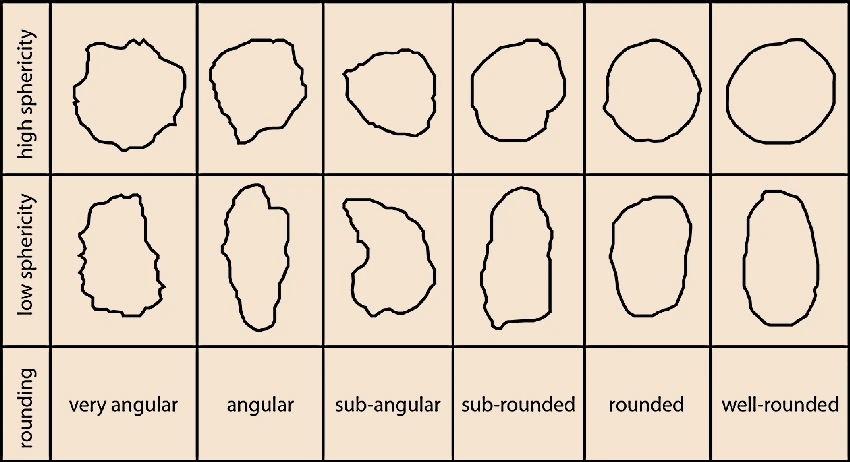
Image Source: Research Paper
Sphericity Formula for Cylinder
For a cylinder with height (h) and radius (r):
\[V = \pi r^2 h\]
\[A = 2 \pi r h + 2 \pi r^2\]
putting the volume and surface area in the general formula of sphericity, we get:
\[\Psi = \frac{\pi^{\frac{1}{3}} \left(6 \pi r^2 h\right)^{\frac{2}{3}}}{2 \pi r h + 2 \pi r^2}\]
for an Ideal cylinder where, Height = 2 Radius, putting the values we get:
\[\Psi = \frac{\pi^{\frac{1}{3}} (6V)^{\frac{2}{3}}}{A}\]
\[\Psi = \frac{\pi^{\frac{1}{3}} \left(6 \cdot 2 \pi r^3\right)^{\frac{2}{3}}}{6 \pi r^2}\]
on simplifying, \(\Psi = 0.873\)
Therefore, the sphericity of a cylinder where the height ( h ) is twice the radius ( r ) is approximately \( \Psi \approx 0.873 \).
Edition: 7th Edition, By: Warren L. McCabe, Julian C. Smith, Peter Harriott
A comprehensive resource on chemical engineering principles, covering core unit operations and practical applications essential for professionals and students alike.
Buy on AmazonSphericity Formula for Cuboid/Cube
For a perfect cube with side length (a):
\[V = a^3\]
\[A = 6a^2\]
putting the volume and surface area in the general formula of sphericity, we get:
\[\Psi = \frac{\pi^{\frac{1}{3}} \left(6 a^3\right)^{\frac{2}{3}}}{6 a^2}\]
on simplifying, \(\Psi = 0.806\)
Therefore, the sphericity of a perfect cube is \(\Psi \approx 0.806\).
| Particle Shape | Surface Area, (\(A_p\)) | Volume, (\(V_p\)) |
|---|---|---|
| Sphere | \( 4\pi r^2 \) | \( \frac{4}{3} \pi r^3 \) |
| Cube | \( 6a^2 \) | \( a^3 \) |
| Cuboid | \( 2(lw + lh + wh) \) | \(l \times w \times h \) |
| Cylinder | \( 2\pi r (r + h) \) | \( \pi r^2 h \) |
The sphericity (\Psi) for a cuboid with dimensions (a), (b), and (c) is given by:
\[\Psi = \frac{\pi^{\frac{1}{3}} \left(6abc\right)^{\frac{2}{3}}}{2(ab + bc + ca)}\]
To get the sphericity values of common objects: Wikipedia- Sphericity Values of common objects
Here we are providing the commonly used sphericity values for different particles in the table provided below:
| Particle | Sphericity \(\Psi\) |
|---|---|
| Crushed coal | 0.75 |
| Crushed sandstone | 0.8–0.9 |
| Round sand | 0.92–0.98 |
| Crushed glass | 0.65 |
| Mica flakes | 0.28 |
| Sillimanite | 0.75 |
| Common salt | 0.84 |
Source: Particle characterization for fluidized bed combustion
Related: Ergun Equation Calculator for Pressure Drop in Packed Bed Column
Related: Head Loss or Pressure Loss Calculator using Darcy-Weisbach Equation
Edition: 9th Edition, By: Don W. Green, Marylee Z. Southard
The ultimate resource for chemical engineering, covering core concepts, data, and insights. An invaluable reference for students, engineers, and industry professionals.
Buy on AmazonExample Problem on Sphericity Calculation
Estimate the Sphericities \((a)\) A cylindrical needle with height ( h ) equal to 5 times the diameter. \((b)\) A rectangular prism with sides \( a \), \( 2a \), and \( 3a \)?
a) First calculating the volume and surface area for the given parameter \(h = 5d\) or \(h=10r\), where r is the radius and h is height of the cylinder.
The volume ( V ) of a cylinder is given by \(V = \pi r^2 h \)
Substituting ( h = 10r ),
\(V = \pi r^2 \cdot 10r = 10 \pi r^3 \)
The total surface area ( A_{\text{total}} ) of the cylinder is:
\( A_{\text{total}} = 2 \pi r^2 + 2 \pi r h\)
\(A_ {\text{total}} = 2 \pi r^2 + 20 \pi r^2 = 22 \pi r^2 \)
replacing the values of Volume and Surface area in the general formula for sphericity, \(\Psi = \frac{\pi^{\frac{1}{3}} (6V)^{\frac{2}{3}}}{A}\)
\(\Psi = \frac{\pi^{\frac{1}{3}} \left(6 \cdot10 \pi r^3\right)^{\frac{2}{3}}}{22 \pi r^2 }\)
therefore, on solving, \(\Psi = 0.696\)
b) Given, A rectangular prism with sides
- \(length = a \)
- \(breadth = 2a \)
- \(width = 3a \)
First, we will calculate the volume and surface area with the given dimensions, we get
The volume ( V ) of the cuboid is:
\(V = a \times 2a \times 3a = 6a^3\)
The surface area ( A ) of the cuboid is \(A = 2(ab + bc + ca)\) where ( a = a ), ( b = 2a ), and ( c = 3a )
\(A = 2(a \cdot 2a + 2a \cdot 3a + 3a \cdot a)\)
\(A = 2(2a^2 + 6a^2 + 3a^2) = 22a^2\)
replacing the values of Volume and Surface area in the general formula for sphericity, \(\Psi = \frac{\pi^{\frac{1}{3}} (6V)^{\frac{2}{3}}}{A}\)
\(\Psi = \frac{\pi^{1/3} (6 \cdot 6a^3)^{2/3}}{22a^2}\)
therefore, on solving, \(\Psi = 0.7258\)
Resources:
- “Unit Operations in Chemical Engineering” (McCabe et al.)
- “Particle Technology and Separation Processes” (Richardson et al.)
- “Chemical Engineering Design: Principles, Practice and Economics of Plant and Process Design” (Towler and Sinnott)
Disclaimer: The Solver provided here is for educational purposes. While efforts ensure accuracy, results may not always reflect real-world scenarios. Verify results with other sources and consult professionals for critical applications. Contact us for any suggestions or corrections