Screen Analysis – Differential and Cumulative Distribution

Screen analysis, also known as sieve analysis or particle size analysis, is a method used to determine the particle size distribution of a granular material. This process involves passing the material through a series of sieves with progressively smaller mesh sizes to separate and classify the particles based on their size.

Related: Sphericity Calculator for different shapes

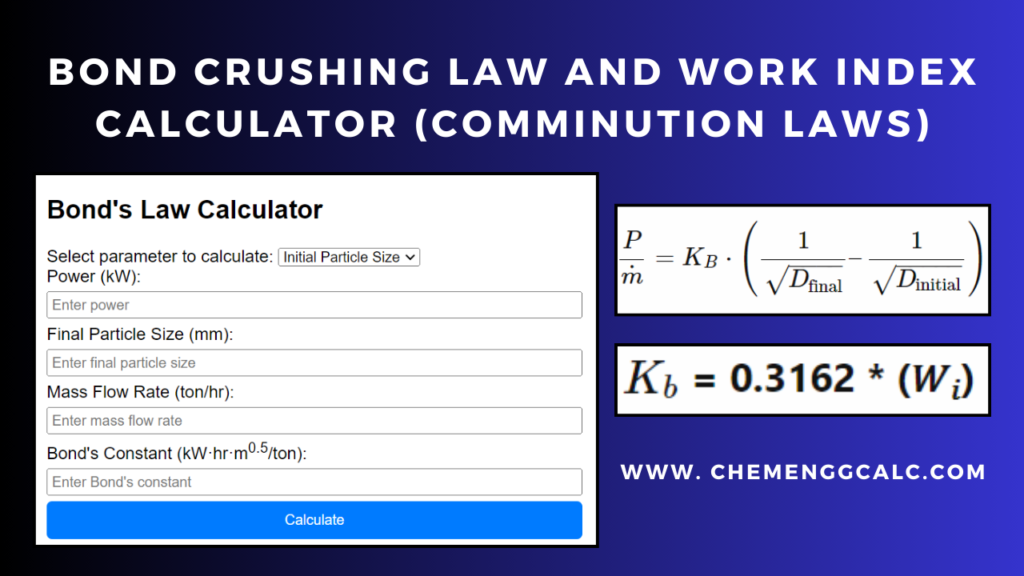
Screen Analysis Calculator for Differential and Cumulative Distribution

This Screen Analysis Tool helps to plot the particle size distribution based on Differential and Cumulative Analysis. In the table given below column of mesh data, including mesh size, screen opening, and mass fraction retained are given which user can change and see the output from the calculated data.

Note: The chart updates in real-time based on the input data, which then provides the visual representation of the average particle size distribution and cumulative analysis.

How to Use this Calculator : Change the values present in the red – Mesh, Screen Opening and Mass Fraction retained. To make this calculator more versatile, we have used the standard screen sizes.

Related: Rittinger’s Law Calculator

Related: Kick’s Law Calculator

Related: Sphericity Calculator for different shapes

Python Code for Screen Analysis

This python code helps user to perform a screen analysis on a dataset that represents particle size distribution. The plot helps visualize the distribution of particle sizes in terms of both differential and cumulative analysis.

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

# Define the data
data = {
    "Mesh": [4, 6, 8, 10, 14, 20, 28, 35, 48, 65, 100, 150, 200, 'Pan'],
    "Screen Opening (D_i in mm)": [4.6990, 3.3270, 2.3620, 1.6510, 1.1680, 0.8330, 0.5890, 0.4178, 0.2950, 0.2080, 0.1470, 0.1040, 0.0740, 0.0000],
    "Mass fraction retained (x_i)": [0.0000, 0.0251, 0.1250, 0.3207, 0.2570, 0.1590, 0.0538, 0.0210, 0.0102, 0.0077, 0.0058, 0.0041, 0.0031, 0.0075],
    "Average particle diameter (D_i in mm)": [np.nan, 4.0130, 2.8445, 2.0065, 1.4095, 1.0005, 0.7110, 0.5034, 0.3564, 0.2515, 0.1775, 0.1255, 0.0890, 0.0370]
}

# Create a DataFrame
df = pd.DataFrame(data)

# Calculate cumulative mass fraction retained
df['Cumulative mass fraction retained'] = df['Mass fraction retained (x_i)'].cumsum()

# Calculate cumulative percentage finer
df['Cumulative percentage finer'] = (1 - df['Cumulative mass fraction retained']) * 100

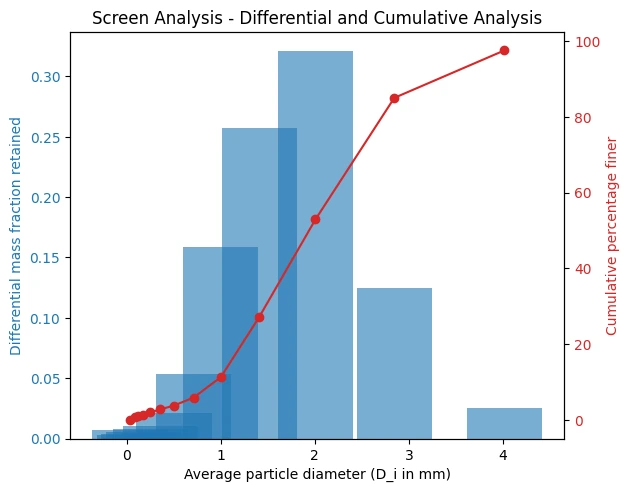
# Differential and Cumulative Analysis Plot
fig, ax1 = plt.subplots()

color = 'tab:blue'
ax1.set_xlabel('Average particle diameter (D_i in mm)')
ax1.set_ylabel('Differential mass fraction retained', color=color)
ax1.bar(df['Average particle diameter (D_i in mm)'], df['Mass fraction retained (x_i)'], color=color, alpha=0.6)
ax1.tick_params(axis='y', labelcolor=color)

ax2 = ax1.twinx()
color = 'tab:red'
ax2.set_ylabel('Cumulative percentage finer', color=color)
ax2.plot(df['Average particle diameter (D_i in mm)'], df['Cumulative percentage finer'], color=color, marker='o')
ax2.tick_params(axis='y', labelcolor=color)

fig.tight_layout()
plt.title('Screen Analysis - Differential and Cumulative Analysis')
plt.show()

Output:

Standard Screen Sizes (Mesh Number conversion)

Standard Screens are used to measure the size and the distribution of particles in the size range between about 3 and 0.0015 inches (76 \(\text{mm}\) and 38 \(\mu\text{m}\)).

Here is the table provide for standard screen with their mesh number and conversions in Inches, mm and Microns.

US Sieve Size	Tyler Equivalent	Opening
		mm	inch	Microns
–	2½ Mesh	8	0.312	8000
–	3 Mesh	6.73	0.265	6730
No. 3½	3½ Mesh	5.66	0.233	5660
No. 4	4 Mesh	4.76	0.187	4760
No. 5	5 Mesh	4	0.157	4000
No. 6	6 Mesh	3.36	0.132	3360
No. 7	7 Mesh	2.83	0.111	2830
No. 8	8 Mesh	2.38	0.0937	2380
No.10	9 Mesh	2	0.0787	2000
No. 12	10 Mesh	1.68	0.0661	1680
No. 14	12 Mesh	1.41	0.0555	1410
No. 16	14 Mesh	1.19	0.0469	1190
No. 18	16 Mesh	1	0.0394	1000
No. 20	20 Mesh	0.841	0.0331	841
No. 25	24 Mesh	0.707	0.0278	707
No. 30	28 Mesh	0.595	0.0234	595
No. 35	32 Mesh	0.5	0.0197	500
No. 40	35 Mesh	0.42	0.0165	420
No. 45	42 Mesh	0.354	0.0139	354
No. 50	48 Mesh	0.297	0.0117	297
No. 60	60 Mesh	0.25	0.0098	250
No. 70	65 Mesh	0.21	0.0083	210
No. 80	80 Mesh	0.177	0.007	177
No.100	100 Mesh	0.149	0.0059	149
No. 120	115 Mesh	0.125	0.0049	125
No. 140	150 Mesh	0.105	0.0041	105
No. 170	170 Mesh	0.088	0.0035	88
No. 200	200 Mesh	0.074	0.0029	74
No. 230	250 Mesh	0.063	0.0025	63
No. 270	270 Mesh	0.053	0.0021	53
No. 325	325 Mesh	0.044	0.0017	44
No. 400	400 Mesh	0.037	0.0015	37

Related: Ergun Equation Calculator for Pressure Drop in Packed Bed Column

Related: Average Particle Size Formula for Volume-Surface Mean, Arithmetic Mean, Mass Mean and Volume Mean Diameter

Related: Head Loss or Pressure Loss Calculator using Darcy-Weisbach Equation

Resources

• “Unit Operations in Chemical Engineering” (McCabe et al.)
• “Particle Technology and Separation Processes” (Richardson et al.)
• “Chemical Engineering Design: Principles, Practice and Economics of Plant and Process Design” (Towler and Sinnott)

Disclaimer: The Solver provided here is for educational purposes. While efforts ensure accuracy, results may not always reflect real-world scenarios. Verify results with other sources and consult professionals for critical applications. Contact us for any suggestions or corrections