Kick’s Law of Crushing Calculator – (Comminution Laws)

Kick’s Law of Crushing, one of the fundamental principles in comminution (the process of reducing the size of solid materials), Kick’s law was proposed in 1885 based on stress analysis of plastic deformation within the elastic limit.

Kick’s law states that the work required for crushing a given mass of material is constant for the same reduction ratio, i.e the ratio of the initial particle size to the final particle size.

Kick’s Law can be expressed mathematically as:

\[ \frac{P}{\dot{m}} = K_k \cdot \ln\left(\frac{D_{\text{i}}}{D_{\text{f}}}\right) \]

• \( \frac{P}{\dot{m}} \) is the specific power consumption \( \frac{\text{kW}}{\text{ton/hr}} \) (kilowatts per ton per hour),
• \( K_k \) is the material-specific constant for specific power consumption \( \frac{\text{kW}\cdot\text{hr}}{\text{ton}} \) (kilowatt-hours per ton),
• \( D_{\text{i}} \) is the initial particle size, measured in millimeters (mm),
• \( D_{\text{f}} \) is the final particle size, also measured in millimeters (mm).

Note: Kick’s law has been demonstrated to be applicable within limited ranges of particle sizes, provided that \( K_k \) is calculated experimentally by tests in a machine of the type to be used and with the material to be crushed.

Related: Rittinger’s Law Calculator

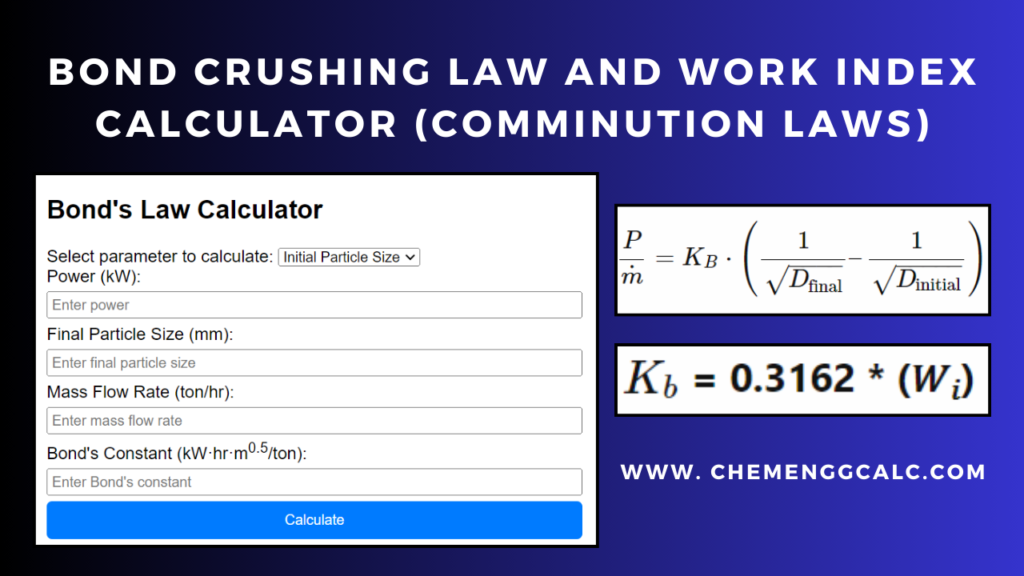
Related: Bond’s Law Calculator and Work Index

Kick’s Law calculator/solver

The Kick’s Law calculator helps user to calculate the energy required for crushing of a solid material based on Kick’s Law. It helps in predicting the energy needed to reduce the size of a given material from a specified initial size to a desired final size.

Related: Sphericity Calculator for different shapes

Example Problem on Kick’s Law

A material is crushed in a Blake jaw crusher such that the average size of particle is reduced from 50 mm to 10 mm with the consumption of energy of 13.0 kW/(Kg/s). what would be consumption of energy needed to crush the same material of average size 75mm to an average of 25 mm, assuming Kick’s law applies to it?

Given Data:

Initial average particle size (\(x_f\)) = 50 mm

Final average particle size (\(x_p\)) = 10 mm

Energy consumed (\(E_1\)) = 13.0 kW/(kg/s)

Calculate Kick’s Law Constant (\(C\)): We’ll use the given data to find the value of \(C\):

\( C = \frac{E_1}{\ln\left(\frac{x_f}{x_p}\right)} \)

Substituting the values: \( C = \frac{13.0}{\ln\left(\frac{50}{10}\right)} = 8.08 \, \text{kW/(kg/s)} \)

Second Scenario: Now, let’s find the energy consumption for the second scenario where the initial average particle size (\(x_f\)) is 75 mm, and the final average particle size (\(x_p\)) is 25 mm.

Using Kick’s Law:

\( E_2 = -C \cdot \ln\left(\frac{x_p}{x_f}\right) \)

Substituting the known values:

\( E_2 = -8.08 \cdot \ln\left(\frac{25}{75}\right) = 8.88 \, \text{kJ/kg} \)

Therefore, the energy required to crush the material from an average size of 75 mm to an average of 25 mm, assuming Kick’s law applies, is approximately 8.88 kJ/kg

Python Code for Kick’s Law / Comminution Laws

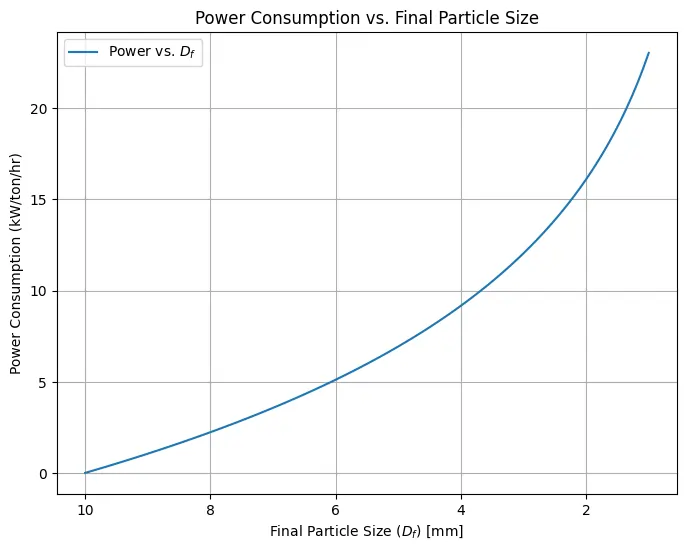
This code calculates the power consumption for size reduction in a crushing process according to Kick’s Law. The initial and final particle sizes of the material being crushed, the mass flow rate of the material, and Kick’s constant are taken then plots the relationship between different values of final size and the corresponding power consumption in kilowatts (kW) for the given process parameters.

Note: This Python code solves the specified problem. Users can copy the code and run it in a suitable Python environment. By adjusting the input parameters, users can observe how the output changes accordingly.

import numpy as np
import matplotlib.pyplot as plt

def power_consumption(Kk, Di, Df):
    """
    Calculate specific power consumption according to Kick's law.
    
    Args:
        Kk (float): Material-specific constant (kWh/ton).
        Di (float): Initial particle size (mm).
        Df (float): Final particle size (mm).
        
    Returns:
        float: Specific power consumption (kW/ton/hr).
    """
    return Kk * np.log(Di / Df)

# Given conditions
Kk = 10  # Material-specific constant (kWh/ton)
Di = 10  # Initial particle size (mm)

# Range of final particle sizes (Df)
Df_values = np.linspace(1, 10, 100)  # Adjust the range as needed

# Calculate power consumption for each Df value
power_values = [power_consumption(Kk, Di, Df) for Df in Df_values]

# Plot
plt.figure(figsize=(8, 6))
plt.plot(Df_values, power_values, label='Power vs. $D_f$')
plt.xlabel('Final Particle Size ($D_f$) [mm]')
plt.ylabel('Power Consumption (kW/ton/hr)')
plt.title('Power Consumption vs. Final Particle Size')
plt.grid(True)

# Reverse x-axis
plt.gca().invert_xaxis()

plt.legend()
plt.show()

Output:

Resources:

• “Unit Operations in Chemical Engineering” (McCabe et al.)
• “Particle Technology and Separation Processes” (Richardson et al.)
• “Chemical Engineering Design: Principles, Practice and Economics of Plant and Process Design” (Towler and Sinnott)

Disclaimer: The Solver provided here is for educational purposes. While efforts ensure accuracy, results may not always reflect real-world scenarios. Verify results with other sources and consult professionals for critical applications. Contact us for any suggestions or corrections.