Table of Contents
When a fluid flow through the pipe or channel the friction is cause due to the factors like surface roughness, flow velocity which leads to head loss or pressure drop across the fluid flow. Engineers use the concept of head loss or pressure loss in designing of various equipment like HVAC system, pipe flow dimensions and fluid transport systems.
Darcy-Weisbach Equation
Darcy-Weisbach equation is the fundamental equation in fluid mechanics which is used to calculate the pressure loss (or head loss) due to friction in a pipe or duct as fluid flows through it.
The Darcy-Weisbach equation for pressure drop (ΔP) due to friction in a pipe is given by:
\[\Delta P = f \cdot \left( \frac{L}{D} \right) \cdot \left( \frac{\rho v^2}{2} \right)\]
The Darcy-Weisbach equation for head loss \((h_f)\) due to friction in a pipe is given by:
\[h_f = f \cdot \left( \frac{L}{D} \right) \cdot \left( \frac{v^2}{2g} \right)\]
where:
- ΔP is the Pressure drop (Pa or N/m²)
- hf is the head loss (m)
- f is the Darcy friction factor (dimensionless)
- L is the Length of the pipe (m)
- D is the Diameter of the pipe (m)
- \(\rho\) is the Fluid density (kg/m³)
- \(v\) is Velocity of the fluid (m/s)
When a fluid flows through a pipe or channel, frictional resistance opposes its motion, which leads to the dissipation of energy and a reduction in pressure intensity along the flow direction which is represented by the Darcy Weisbach Equation.
Related: Newton’s Law of Viscosity Calculator – Dynamic Viscosity
Related: Hagen-Poiseuille Equation Calculator / Poiseuille’s Law Solver
Head Loss or Pressure Loss Calculator
This Head Loss or Pressure Loss Calculator uses the Darcy-Weisbach equation to compute the pressure drop or head loss in a fluid flowing through a pipe. User can input the pipe length, diameter, fluid velocity, density, and friction factor, then select whether to calculate pressure loss or head loss.
Related: Bernoulli’s Equation Calculator / Solver – Interactive Python Code
Related: Centrifugal Pump Sizing Calculation – TDH, NPSHa vs Flow Rate curve & Power Required
Friction Factor Calculation
The friction factor \(f\) also known as Darcy-Weisbach Friction Factor is a dimensionless quantity that represents the frictional resistance or energy loss due to shear forces between fluid layers as the fluid flows through a pipe or channel.
There is another form of friction factor known as Fanning Friction Factor \((f_F)\) which is typically 1/4th of the Darcy friction factor \((f_F=\frac{f}{4})\) used in different industries.
Related: Friction Factor Calculator Moody’s Diagram for Smooth and Rough Pipes
Friction Factor depends on the Reynolds number (Re) and the relative roughness of the pipe:
- In laminar flow, \(f= \frac{64}{Re}\), where Re is the Reynolds number.
- In turbulent flow, \(f\) is determined by empirical formulas like the Colebrook-White equation or Moody charts.
Colebrook-White Equation:
\[\frac{1}{\sqrt{f}} = -2 \log_{10} \left( \frac{\epsilon/D}{3.7} + \frac{2.51}{Re \sqrt{f}} \right)\]
where:
- \(f\) if Darcy-Weisbach friction factor (dimensionless)
- \( \epsilon \) represents Pipe roughness height (m)
- D is Diameter of the pipe (m)
- Re is Reynolds number (dimensionless)
- \( \log_{10} \) is Base-10 logarithm
Edition: Revised 2nd Edition, By: R. Byron Bird, Warren E. Stewart, Edwin N. Lightfoot
Comprehensive coverage of transport phenomena, including momentum, heat, and mass transfer. Updated content for better clarity.
Buy on AmazonRelated: Stoke’s Law Calculator for Terminal Velocity – Derivation and Python Code
Example Problem on Darcy-Weisbach Equation
Design the diameter of a steel pipe to carry oil having kinematic viscosity of 0.20 stokes with a velocity of 1.5 m/s, if Darcy’s friction factor over almost the whole turbulent range is given by
\[ f = 0.0055 \left[1 + \left(20000 \frac{\varepsilon}{D} + \frac{10^6}{Re}\right)^{0.33}\right] \]
in which \(\varepsilon\) = equivalent sand grain roughness, D = diameter of pipe, Re = Reynolds number. The head loss is to be limited to 0.4 m per 100 metres of pipe. The equivalent sand grain roughness for steel may be assumed as 0.045 mm.
Solution:
Given:
- Oil kinematic viscosity, υ = 0.20 stokes
- Velocity of oil, V = 1.5 m/s
- Darcy’s friction factor equation: f = 0.0055 [1 + (20000 ε/D + 10⁶/Re)⁰·³³] where ε = equivalent sand grain roughness D = diameter of pipe Re = Reynolds number
- Head loss limit, \(h_f\) = 0.4 m per 100 metres of pipe
- Equivalent sand grain roughness for steel, ε = 0.045 mm
For the diameter, D of the pipe, Reynolds number is:
Re = VD/υ = (1.5 × D) / (0.20 × 10⁻⁴)
Re = 7.5 × 10⁴ D
given, ε = 0.045 mm = 0.045 × 10⁻³ m
Substituting these values in the given expression for f it becomes
\[f = 0.0055 \left[1 + \left(\frac{0.9}{D} + \frac{13.33}{D}\right)^{0.33}\right]\]
or
\[f = 0.0055 + \frac{0.0132}{D^{0.33}} \quad … (i)\]
Using Darcy-Weisbach equation
\[h_f = \frac{fLV^2}{2gD}\]
\[\frac{0.4}{100} = \frac{f \times (1.5)^2}{2 \times 9.81 \times D}\]
\[f = 0.0349 D \quad … (ii)\]
thereby solving equations (i) and (ii) by hit & trail method, value of D can be calculated. For ease of solving, we are using python to solve the given set the equations
import numpy as np
from scipy.optimize import fsolve
# Define the system of equations
def equations(vars):
D = vars # D is the diameter we want to solve for
# Equation (i)
f1 = 0.0055 + 0.0132 / (D ** 0.33) - f2(D)
return f1
# Define Equation (ii) separately as f2(D)
def f2(D):
return 0.0349 * D
# Initial guess for D
D_guess = 0.1 # A reasonable initial guess for the diameter
# Solve the system of equations
D_solution = fsolve(equations, D_guess)
# Print the solution
print(f'The solution for the diameter D is: {D_solution[0]:.5f} meters')Output: The solution for the diameter D is: 0.60423 meters
Therefore, we get the value of diameter to be 0.604 meters. However, if the pipe of diameter 0.604 m is not available, the next larger standard size of the pipe may be used.
Also Read: Chemical Engineering as a career option in India
Python Code for Head Loss Calculation
This python code helps user to calculate the pressure loss and head loss in a pipe using the Darcy-Weisbach equation for varying pipe diameters at different values of friction factors (showing smooth or rough pipes).
Note: This Python code solves the specified problem. Users can copy the code and run it in a suitable Python environment. By adjusting the input parameters, users can observe how the output changes accordingly.
import numpy as np
import matplotlib.pyplot as plt
# Define constants
g = 9.81 # acceleration due to gravity (m/s²)
rho = 1000 # density of water (kg/m³) - assuming water
L = 100 # pipe length (m)
v = 2 # flow velocity (m/s)
# Realistic friction factors for different scenarios (smooth pipe, rough pipe, etc.)
friction_factors = [0.01, 0.02, 0.03, 0.04, 0.05]
# Define function to calculate pressure loss and head loss
def calculate_losses(D, f):
# Pressure loss (Pa)
delta_P = f * (L / D) * (rho * v**2 / 2)
# Head loss (m)
h_f = delta_P / (rho * g)
return delta_P, h_f
# Pipe diameters (m) for calculations
diameters = np.linspace(0.01, 0.5, 50) # diameters from 0.01m to 0.5m
# Initialize lists to store results for different friction factors
pressure_losses = {f: [] for f in friction_factors}
head_losses = {f: [] for f in friction_factors}
# Calculate pressure loss and head loss for varying diameters and friction factors
for f in friction_factors:
for D in diameters:
dp, hf = calculate_losses(D, f)
pressure_losses[f].append(dp)
head_losses[f].append(hf)
# Plot results
plt.figure(figsize=(12, 6))
# Plot for pressure loss vs pipe diameter
plt.subplot(1, 2, 1)
for f in friction_factors:
plt.plot(diameters, pressure_losses[f], label=f'f = {f}')
plt.xlabel('Pipe Diameter (m)')
plt.ylabel('Pressure Loss (Pa)')
plt.title('Pressure Loss vs Pipe Diameter')
plt.legend()
plt.grid(True)
# Plot for head loss vs pipe diameter
plt.subplot(1, 2, 2)
for f in friction_factors:
plt.plot(diameters, head_losses[f], label=f'f = {f}')
plt.xlabel('Pipe Diameter (m)')
plt.ylabel('Head Loss (m)')
plt.title('Head Loss vs Pipe Diameter')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()Output:
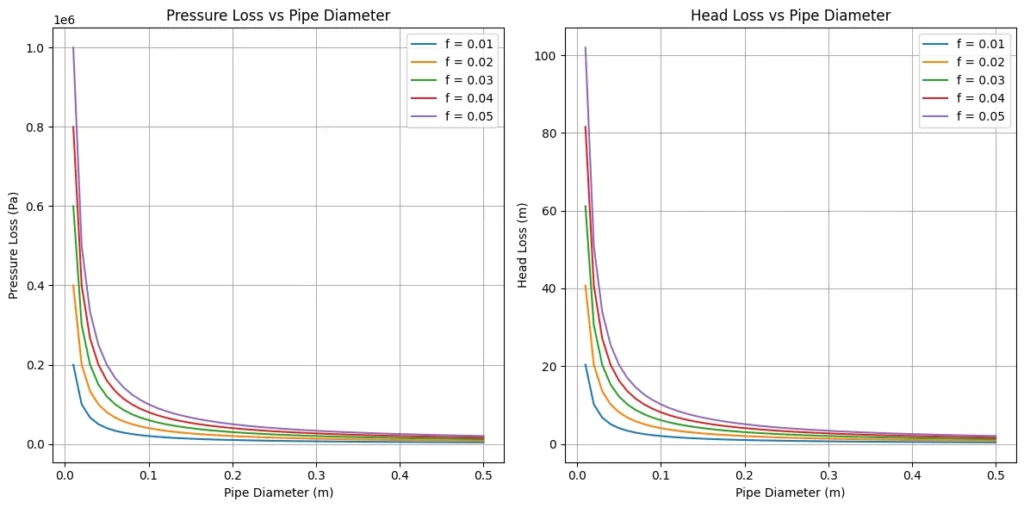
Resources
- “Fluid Mechanics” by Frank M. White
- “Introduction to Fluid Mechanics” by Robert W. Fox, Alan T. McDonald, and Philip J. Pritchard
- “Principles of Heat and Mass Transfer” by Frank P. Incropera and David P. DeWitt
- Python.org – The official Python website offers tutorials, documentation, and resources for learning Python.
Disclaimer: The Solver provided here is for educational purposes. While efforts ensure accuracy, results may not always reflect real-world scenarios. Verify results with other sources and consult professionals for critical applications. Contact us for any suggestions or corrections.







I always appreciate how you take the time to explore both the pros and cons of an issue. It gives your content a well-rounded feel that’s rare these days.