Table of Contents
What is Froude Number?
The Froude number (Fr) is a dimensionless number which is used to characterizes the flow of fluids. It is named after the British engineer William Froude.
The Froude number is defined as the ratio of inertia force to the gravitational forces in fluid dynamics. This number is important in the study of open channel flows, ship hydrodynamics, and the behavior of flow around objects.
Mathematically, it is defined as:
\[\text{Fr} =\frac{\text{Inertial Force}}{\text{Gravitational Force}}\]
\[\text{Fr} = \frac{ \rho u^2 L^2}{\rho g L^3} = \frac{U^2}{g L}\]
\[\text{Fr} = \frac{U}{\sqrt{gL}}\]
where:
- \(U\) is the characteristic velocity of the flow
- \(g\) is the acceleration due to gravity
- \(L\) is the characteristic length
Related: Newton’s Law of Viscosity Calculator – Dynamic Viscosity
Related: Hagen-Poiseuille Equation Calculator / Poiseuille’s Law Solver
Froude Number Calculator
This Calculator is a web tool designed to compute the Froude number. User are able to input values for velocity (U), and characteristic length (L), and then it performs the calculation which helps in understanding flow regime in open channel and around objects.
Related: Other Dimensionless Numbers
Related: Hydraulic Diameter Calculator for Circular and Non-Circular cross-section
Significance of Froude Number
The Fr number is used to categorize and understand different flow regimes based on their velocity relative to the speed of surface waves. It is helpful for engineers and scientists to predict and design structures and systems that interact with flowing fluids, ensuring safety, efficiency, and optimal performance.
Case 1. Subcritical Flow or Tranquil Flow (Fr < 1)
In this regime, the flow velocity is slower than the speed of gravity waves that would propagate along the surface of the fluid. For example, A calm and slow-moving sections of the river where the flow is controlled by downstream conditions.
Case 2. Critical Flow (Fr = 1)
This is the point when the flow velocity is equal to the speed of the surface gravity waves. For example, Critical flow often occurs over weirs or sharp changes in the river bed where significant energy transformations occur.
Case 3. Supercritical Flow (Fr > 1)
The flow velocity is faster than the speed at which surface gravity waves propagate. For example, Supercritical flow can occur in rapidly flowing rivers or when fluid accelerates rapidly downhill.

Froude Number Applications
The Froude Number (Fr) is an important dimensionless parameter in fluid mechanics, which is widely used to characterize and analyze different flow regimes across various engineering and environmental applications.
- In Ship Design and Naval Architecture, Fr number helps to determine the optimal speed of a ship and ensures stable operation in different sea conditions. A low Fr Number results in lower wave resistance (subcritical flow), whereas high Fr number leads to higher wave resistance (supercritical flow).
- The stability of hydraulic structures, such as dams and spillways, Supercritical flows (Fr > 1) can cause turbulent conditions that might damage these structures, requiring careful design considerations.
- In Atmospheric and Oceanic flows, the Fr Number is used to analyze the stability of stratified flows, such as the flow of air over mountains or the flow of ocean currents over underwater topography.
Other Dimensionless Numbers
Here we have tabulated the list of dimensionless numbers which are commonly used in Chemical Engineering with their formula, definition, and significance.
| Dimensionless Number | Formula | Definition | Significance |
|---|---|---|---|
| Reynolds Number (Re) | \[\text{Re} = \frac{\rho u L}{\mu} = \frac{u L}{\nu}\] | Ratio of inertial forces to viscous forces. | Determines flow regime: Re < 2000: Laminar flow Re > 4000: Turbulent flow. Critical for pipe flow and reactors. |
| Prandtl Number (Pr) | \[\text{Pr} = \frac{C_p \mu}{k}\] | Ratio of momentum diffusivity to thermal diffusivity. | It indicates the relative thickness of momentum and thermal boundary layers in heat transfer. |
| Nusselt Number (Nu) | \[\text{Nu} = \frac{h L}{k}\] | Ratio of convective to conductive heat transfer. | It is used in convective heat transfer problems to evaluate heat transfer coefficients. |
| Sherwood Number (Sh) | \[\text{Sh} = \frac{k_m L}{D}\] | Ratio of convective to diffusive mass transfer. | It is important in mass transfer, especially in diffusion and absorption processes. |
| Péclet Number (Pe) | \[\text{Pe} = \text{Re} \cdot \text{Pr}\] | Ratio of advection to diffusion. Combines Reynolds and Prandtl numbers. | It is important in heat and mass transfer processes where advection dominates over diffusion. |
| Schmidt Number (Sc) | \[\text{Sc} = \frac{\mu}{\rho D}\] | Ratio of momentum diffusivity to mass diffusivity. | It is used in mass transfer to relate momentum and mass transport. Analogous to the Prandtl number in heat transfer. |
| Lewis Number (Le) | \[\text{Le} = \frac{\alpha}{D} = \frac{\text{Sc}}{\text{Pr}}\] | Ratio of thermal diffusivity to mass diffusivity. | It relates thermal and mass transport; Le = 1 implies similar thermal and mass diffusivity. |
| Fourier Number (Fo) | \[\text{Fo} = \frac{\alpha t}{L^2}\] | Ratio of heat conduction rate to heat storage rate. | It is used in unsteady-state heat transfer problems, like transient conduction. |
| Biot Number (Bi) | \[\text{Bi} = \frac{h L}{k}\] | Ratio of internal thermal resistance to surface thermal resistance. | It determines whether heat conduction is lumped or distributed. Bi < 0.1: Lumped system approximation valid. |
| Weber Number (We) | \[\text{We} = \frac{\rho u^2 L}{\sigma}\] | Ratio of inertial forces to surface tension forces. | It is important in multiphase flows, droplet formation, and fluid interface stability. |
| Capillary Number (Ca) | \[\text{Ca} = \frac{\mu u}{\sigma}\] | Ratio of viscous forces to surface tension forces. | It is used to study the behavior of capillary flows and thin-film phenomena. |
| Froude Number (Fr) | \[\text{Fr} = \frac{u^2}{g L}\] | Ratio of inertial forces to gravitational forces. | It is important in free-surface flows, mixing, and fluidized bed design. |
| Damköhler Number (Da) | \[\text{Da} = \frac{\text{Reaction rate}}{\text{Flow rate}}\] | Ratio of chemical reaction time to residence time. | It is important in chemical reaction engineering; determines if a process is reaction- or transport-limited. |
| Thiele Modulus (ϕ) | \[\phi = L \sqrt{\frac{k}{D}}\] | Ratio of reaction rate to diffusion rate within a catalyst particle. | It is used in heterogeneous catalysis to determine diffusion limitations within catalyst pores. |
| Knudsen Number (Kn) | \[\text{Kn} = \frac{\lambda}{L}\] | Ratio of molecular mean free path to characteristic length. | It is important in gas flow through small pores or microchannels; indicates continuum vs. molecular flow regime. |
| Eckert Number (Ec) | \[\text{Ec} = \frac{u^2}{C_p \Delta T}\] | Ratio of kinetic energy to enthalpy difference. | It is used in high-speed flows and heat transfer problems involving viscous dissipation. |
| Grashof Number (Gr) | \[\text{Gr} = \frac{g \beta \Delta T L^3}{\nu^2}\] | Ratio of buoyancy forces to viscous forces. | It determines the importance of natural convection in heat transfer problems. |
| Stanton Number (St) | \[\text{St} = \frac{h}{\rho u C_p}\] | Ratio of heat transfer coefficient to the product of fluid velocity and specific heat. | It is used in heat transfer to describe convective heat transfer efficiency relative to bulk flow. |
Related: 10 Mostly used Dimensionless Numbers in Chemical Engineering
Python Code for Froude Number Calculation
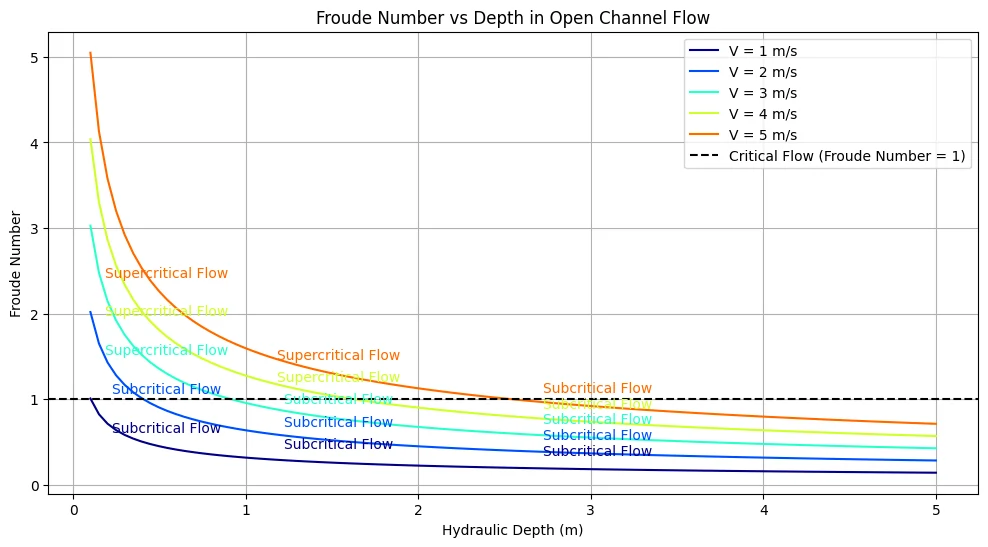
This Python script helps user to visualize how the Froude number (Fr) varies with hydraulic depth in an open channel flow at different velocities. Each velocity is represented by a line plot where colors distinguish different velocities, and annotations on the plot indicate the flow regime at specific depths.
Note: This Python code solves the specified problem. Users can copy the code and run it in a suitable Python environment. By adjusting the input parameters, and observe how the output changes accordingly.
import numpy as np
import matplotlib.pyplot as plt
def calculate_froude_number(V, g, depth):
return V / np.sqrt(g * depth)
# Define parameters
g = 9.81 # Acceleration due to gravity (m/s^2)
depths = np.linspace(0.1, 5, 100) # Depths in the open channel (m)
velocities = [1, 2, 3, 4, 5] # Velocities (m/s)
# Plot Froude number vs depth for each velocity with different colors
plt.figure(figsize=(12, 6))
for i, V in enumerate(velocities):
froude_numbers = calculate_froude_number(V, g, depths)
flow_types = []
for fn in froude_numbers:
if fn < 1:
flow_types.append('Subcritical Flow')
elif fn == 1:
flow_types.append('Critical Flow')
else:
flow_types.append('Supercritical Flow')
color = plt.cm.jet(i / len(velocities)) # Jet colormap for distinct colors
plt.plot(depths, froude_numbers, label=f'V = {V} m/s', color=color)
# Annotate flow regime at specific depths
annotate_depths = [0.5, 1.5, 3.0] # Depths to annotate
for depth in annotate_depths:
index = np.argmin(np.abs(depths - depth)) # Find index closest to desired depth
plt.annotate(flow_types[index], (depth, froude_numbers[index]),
textcoords="offset points", xytext=(5,10), ha='center', color=color)
plt.xlabel('Hydraulic Depth (m)')
plt.ylabel('Froude Number')
plt.title('Froude Number vs Depth in Open Channel Flow')
plt.axhline(y=1, color='black', linestyle='--', label='Critical Flow (Froude Number = 1)')
plt.legend()
plt.grid(True)
plt.show()
Output:
Resources
- “Fluid Mechanics” by Frank M. White
- “Introduction to Fluid Mechanics” by Robert W. Fox, Alan T. McDonald, and Philip J. Pritchard
- “Principles of Heat and Mass Transfer” by Frank P. Incropera and David P. DeWitt
- Python.org – The official Python website offers tutorials, documentation, and resources for learning Python.
Disclaimer: The Solver provided here is for educational purposes. While efforts ensure accuracy, results may not always reflect real-world scenarios. Verify results with other sources and consult professionals for critical applications. Contact us for any suggestions or corrections.