Table of Contents
In chemical reaction engineering, conversion, selectivity, and yield are essential metrics that help evaluate the efficiency and effectiveness of chemical processes, particularly in systems involving multiple reactions and is a key for making industrial processes efficient and profitable.
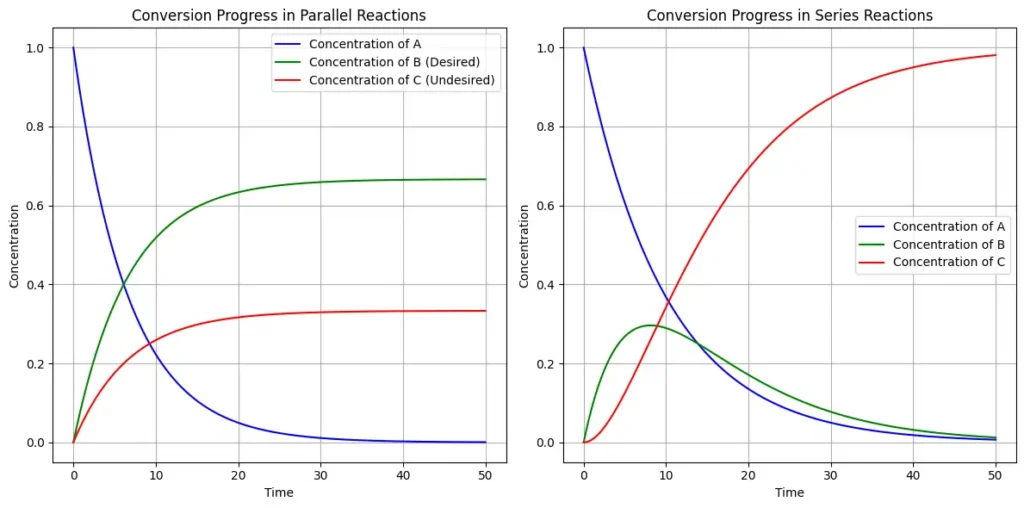
A multiple reaction involves more than one chemical reaction occurring simultaneously in a reactor. These can be classified as parallel reactions or series reactions.
- A parallel reaction where a single reactant produces multiple products through different pathways.
\[A \overset{k_1}{\longrightarrow} B \, (\text{desired})\] \[A \overset{k_2}{\longrightarrow} C \, (\text{undesired})\]
- A series reactions, where a reactant is converted into an intermediate that further reacts to form another product.
\[A \overset{k_1}{\longrightarrow} B \overset{k_2}{\longrightarrow} C\]
Multiple reactions are important for optimizing reactor design and maximizing desired product yields while minimizing by-products.
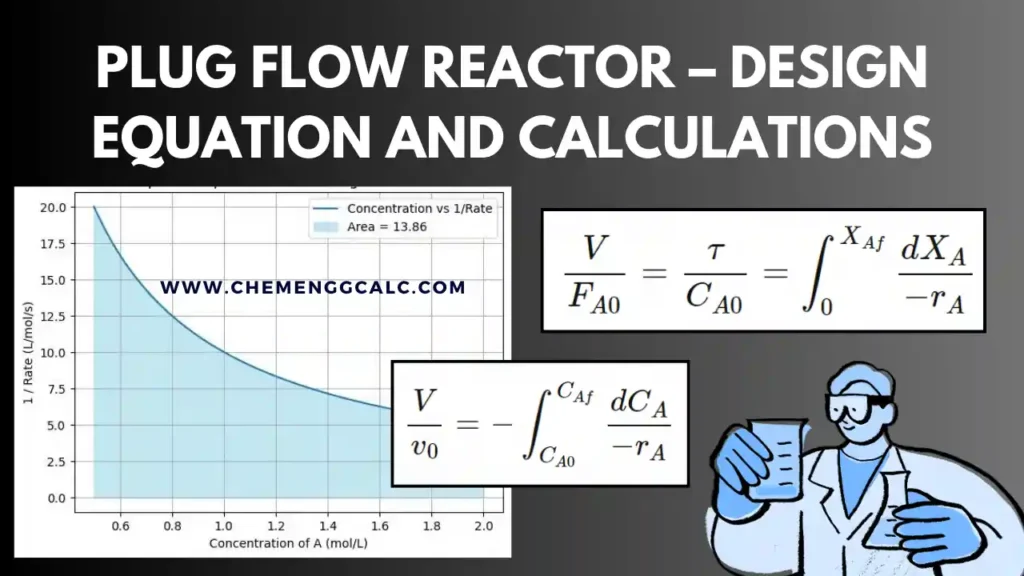
Related: Plug Flow Reactor – Design Equation and Calculations
Related: Arrhenius Equation Calculator for Activation Energy
Conversion – Meaning and Significance
Conversion in a chemical reaction is a measure of how much of a reactant has been transformed into products during a chemical reaction. It is usually expressed as a fraction or percentage of the initial amount of reactant that has been consumed.
The conversion (X) can be calculated using the following formula:
\[ X = \frac{\text{Amount of reactant consumed}}{\text{Initial amount of reactant}} \]
Alternatively, in terms of concentration, the formula is represented as:
\[ X = \frac{C_0 – C}{C_0} \]
where,
- \( C_0 \) is the initial concentration of the reactant
- \( C \) is the final concentration of the reactant.
Note: Conversion is an important metric in a chemical reaction which tells how much a reaction has progressed. Conversion values range from 0 to 1 (or 0% to 100%), indicating the extent of reaction completion.
A high conversion means the reactant has consumed efficiently, while a low conversion means the reactant is not consumed efficiently indicates that the reaction conditions need optimization.
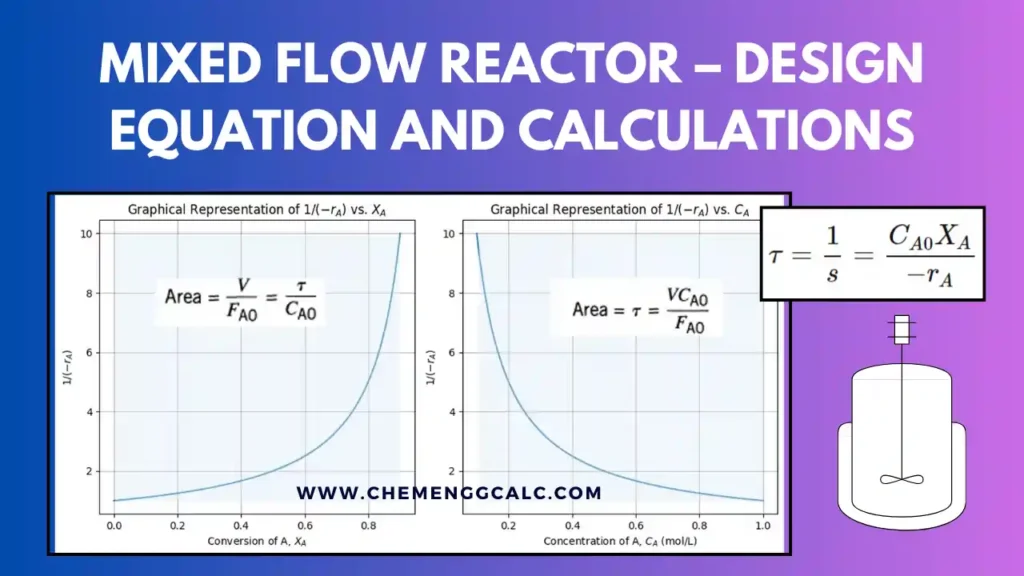
Related: Performance Equation for Mixed Flow Reactor
Related: C Curve, E Curve and F Curve from Pulse or Step Input Tracer in Non Ideal Reactor
Selectivity – Meaning and Significance
Selectivity is a measure of how efficiently the reactants are converted into the desired product in comparison to unwanted by-products.
For a parallel reaction \[A \overset{k_1}{\longrightarrow} B \, (\text{desired})\] \[A \overset{k_2}{\longrightarrow} C \, (\text{undesired})\]
Selectivity is an important metric for a multiple reaction and is expressed as the ratio of the moles of the desired product to the moles of the undesired product. It can expressed in two forms as instantaneous selectivity and overall selectivity.
– Instantaneous Selectivity
This is defined as the ratio of the rate of formation of a desired product to the rate of formation of an undesired product at a specific moment in time.
Mathematically, it can be expressed as:
\[S_{B/C} = \frac{r_B}{r_C}\]
where \( r_B \) is the rate of formation of the desired product ( B ), and \( r_C \) is the rate of formation of the undesired product ( C ).
- Instantaneous Selectivity is useful in kinetic analysis to identify optimal conditions (e.g., temperature, pressure) that favor the desired product.
- This term is also helpful in selecting appropriate reactor types (e.g., batch vs. continuous) based on how quickly desired products can be formed relative to undesired ones.
Related: PFR and CSTR in Series or Parallel Combination for a single reaction
– Overall Selectivity
Overall Selectivity is defined based on the total amount of products formed at the end of the reaction.
Mathematically, It can be expressed as:
\[S_{B/C} = \frac{n_B}{n_C}\]
where \( n_B \) is the number of moles of the desired product and \( n_C \) is the number of moles of the undesired product produced.
- Overall selectivity provides a combined view of reaction efficiency over time, it quantifies how much desired product formed from given reactants
Edition: 3rd Edition, By: Octave Levenspiel
A classic textbook covering the principles of chemical reaction engineering with detailed analysis of reactor design and kinetics.
Buy on AmazonFractional Yield
Yield is the another metric which quantifies how effectively reactants are converted into desired products. It is defined as the amount of product formed relative to the amount of reactant consumed.
Consider the decomposition of reactant A, and let \(\phi\) be the fraction of A disappearing at any instant which is converted into desired product R. We call this the instantaneous fractional yield of R.
– Instantaneous Fractional Yield (\(\phi\))
This term represents the fraction of reactant A that is converted into the desired product R at any given moment in the reactor.
Mathematically Instantaneous fractional yield is expressed as:
\[ \phi = \frac{\text{moles R formed}}{\text{moles A reacted}} = \frac{dC_R}{-dC_A} \]
where:
- \(C_R\) is the concentration of product R
- \(C_A\) is the concentration of reactant A
Related: Rate Constant Calculation for Zeroth, First and Second Order using Integrated Rate Equations
– Overall Fractional Yield, (\(\Phi\))
This term represents the fraction of all reacted A that has been converted into R over the entire course of the reaction in the reactor. It’s an average of all the instantaneous yields throughout the reactor.
The overall fractional yield \(\Phi\) is defined as:
\[\Phi = \frac{\text{total R formed}}{\text{total A reacted}}\]
\[\Phi = \frac{C_{Rf} – C_{Af}}{C_{A0} – C_{Af}} \]
where:
- \(C_{A0}\) is the initial concentration of A
- \(C_{Af}\) is the final concentration of A
- \(C_{Rf}\) is the final concentration of R
The relationship between \(\Phi\) and \(\phi\) can be expressed as:
\[\Phi = \frac{1}{C_{A0} – C_{Af}} \int_{C_{A0}}^{C_{Af}} \phi dC_A \]
This equation shows that the overall fractional yield is the average of the instantaneous fractional yields over the reaction.
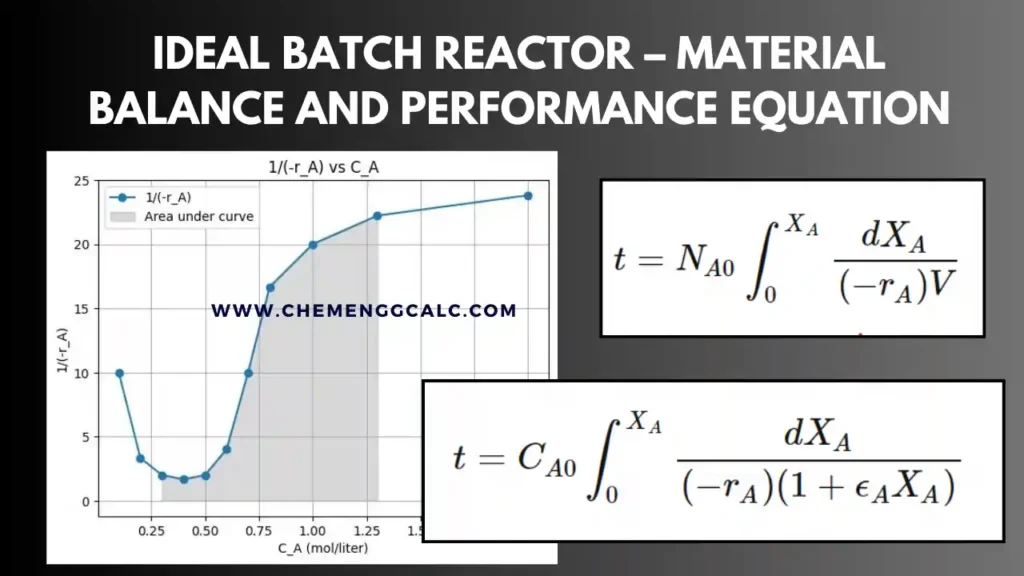
Related: Performance Equation for Ideal Batch Reactor
Resources:
- Chemical Reactor Analysis and Design Fundamentals by Rawlings and Ekerdt
- Elements of Chemical Reaction Engineering by Fogler
- “Chemical Reaction Engineering“ by Octave Levenspiel
Disclaimer: The content provided here is for educational purposes. While efforts ensure accuracy, results may not always reflect real-world scenarios. Verify results with other sources and consult professionals for critical applications. Contact us for any suggestions or corrections.