Table of Contents
A Mixed Flow Reactor (MFR), also known as a Continuous Stirred-Tank Reactor (CSTR) or vat reactor, is a type of chemical reactor in which the reactants are continuously fed into a stirred tank. The impeller inside the tank continuously mixes the reactants, ensuring a uniform composition throughout the reactor. The products are then continuously withdrawn from the tank. Thus, the exit stream from this reactor has the same composition as the fluid within the reactor.
MFRs/CSTRs are usually used in industrial processes where a steady-state operation is desired or where there are continuous reactions occurring. They’re particularly useful when the reaction rate is fast and doesn’t require precise control over reactant concentrations or when the reaction rate is slow and requires a long residence time.

Space-Time and Space-Velocity
Space-time (\(\tau\)) and space-velocity (s) are key performance metrics for flow reactors.
Space-Time (\(\tau\)) is defined as the time required to process one reactor volume of feed measured at specified conditions. It is measured in time (hours or minutes or seconds). A space-time of 5 min means that every 5 min one reactor volume of feed at specified conditions is being treated by the reactor.
\(\tau = \frac{1}{s}\) where, s is the space time.
Space-Velocity (s) is the number of reactor volumes of feed at specified conditions which can be treated at one unit time. It is measured in time-1 (hour-1or minute-1or sec-1). A space-velocity of 2 hr-l means that two reactor volumes of feed at specified conditions are being fed into the reactor per hour.
\(s = \frac{1}{\tau}\) where, \(\tau\) is the space-time.
The values of space-time and space-velocity depends on the conditions selected. If they are of the stream entering the reactor, the relation between s and r and the other pertinent variables is
\[\tau = \frac{1}{s} = \frac{C_{A0}V}{F_{A0}} = \frac{V}{{v_0}}\]
where, \(C_{A0}\) is initial concentration of component A (mol/liter), V is the reactor volume (liter), \(F_{A0}\) Initial molar flow rate of component A (mol/time), \(v_0\) is the volumetric feed rate (liter/time).
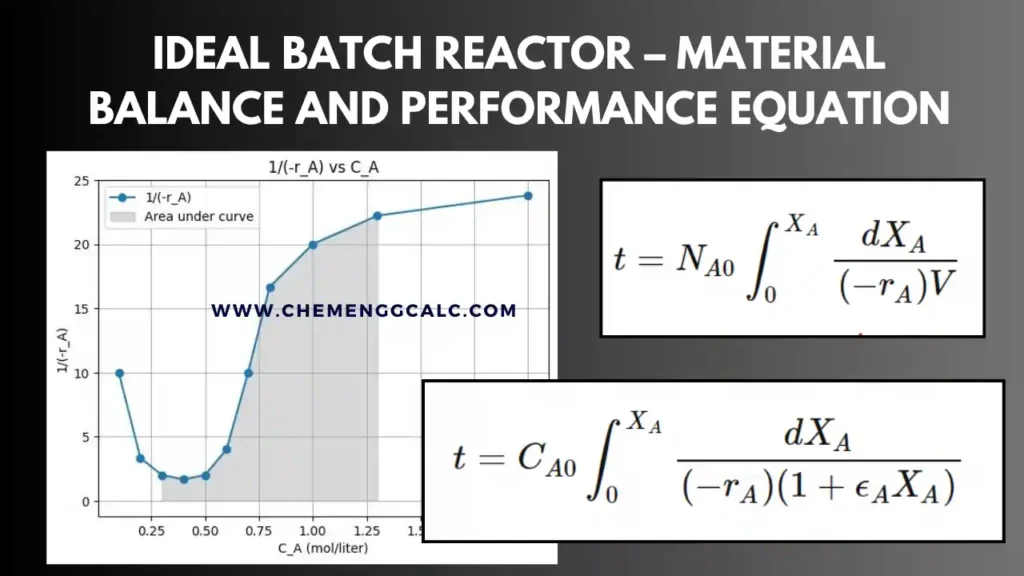
Related: Performance Equation for Ideal Batch Reactor
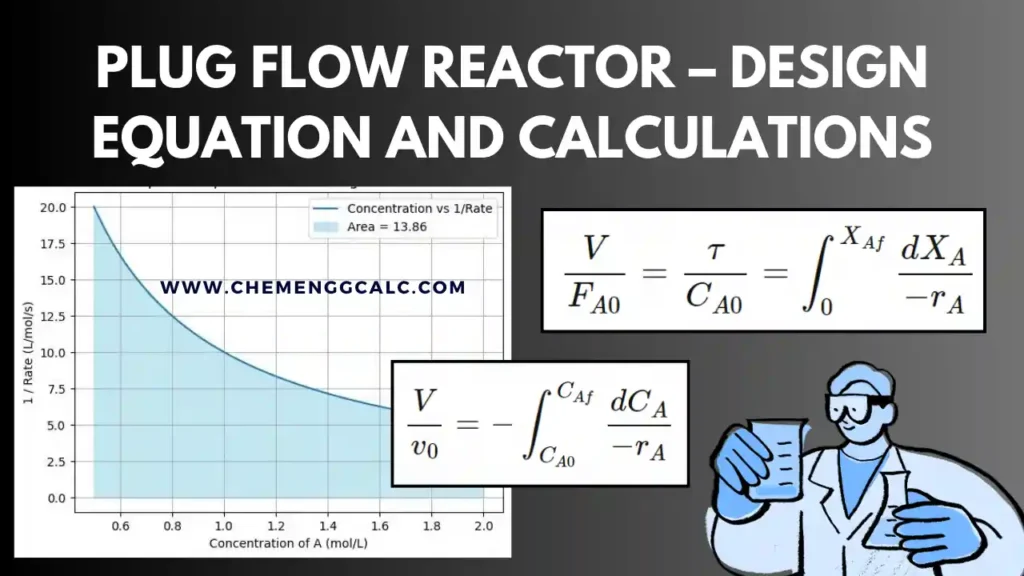
Related: Performance Equation for Plug Flow Reactor
Performance Equation for Mixed Flow Reactor
The starting point for all design is the material balance expressed for any reactant (or product). In case of mixed flow reactor the composition is uniform throughout , the accounting can be made about the reactor as a whole.

Input = Output + Disappearance +Accumulation------- Eq 1
Accumulation = 0 , for steady state
Input of \( A \) (moles/time) = \( F_{A0} \)
Output of \( A \) (moles/time) = \( F_A = F_{A0} (1-X_A) \)
Disappearance of \( A \) by reaction (moles/time) = \( (-r_A) V \) , where \(-r_A\) is rate of reaction with respect to component A
putting these terms in equation 1, we get:
\[F_{A0}{X_A} =(-r_A) V\]
which on rearrangement becomes
\[\frac{V}{F_{A0}} = \frac{X_A}{-r_A} \]
and in terms of space-time \(\tau\) is:
\[\tau = \frac{1}{s} = \frac{C_{A0}X_A}{-r_A} \]
where \(X_A\) and \(r_A\) are measured at exit stream conditions, which are the same as the conditions within the reactor.
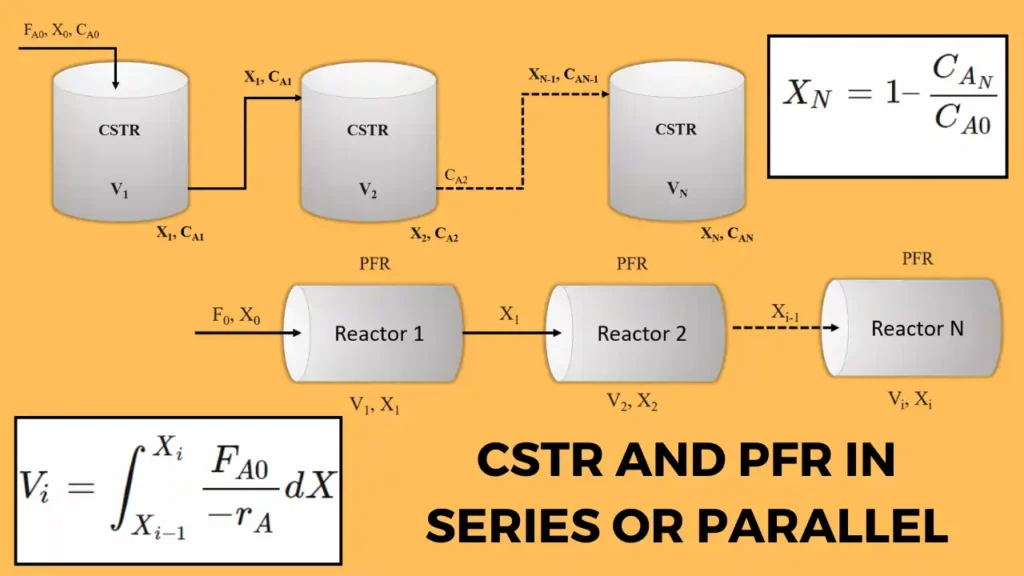
Related: PFR and CSTR in Series or Parallel Combination for a single reaction
Edition: 3rd Edition, By: Octave Levenspiel
A classic textbook covering the principles of chemical reaction engineering with detailed analysis of reactor design and kinetics.
Buy on AmazonPython Code for Mixed Flow Reactor
This code computes the graphical representation of the relationship between the inverse of the reaction rate (1/(−𝑟𝐴) and the conversion of reactant A (𝑋𝐴), as well as the relationship between 1/(−𝑟𝐴)and the concentration of reactant A (𝐶𝐴)
For a mixed flow reactor the area shown in the plot represents \[\frac{V}{F_{A0}} = \frac{X_A}{-r_A} \] for \(( \varepsilon _A = 0\)).
Note: This Python code solves the specified problem for 1st order reaction. Users can copy the code and run it in a suitable Python environment. By adjusting the input parameters, and observe how the output changes accordingly.
import numpy as np
import matplotlib.pyplot as plt
# Define the rate constant (k) and inlet concentration of A (C_A_in)
k = 1 # rate constant
C_A_in = 1.0 # inlet concentration of A
# Create an array of X_A values (conversion of A)
X_A_values = np.linspace(0, 0.9, 100) # 100 points between 0 and 0.9 for X_A
# Calculate -r_A for each X_A value using the rate expression
r_A_values = k * (C_A_in * (1 - X_A_values))
# Calculate 1/(-r_A)
inv_neg_r_A = 1 / (r_A_values)
# Plot 1/(-r_A) versus X_A
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.plot(X_A_values, inv_neg_r_A)
plt.xlabel('Conversion of A, $X_A$')
plt.ylabel('$1/(-r_A)$')
plt.title('Graphical Representation of $1/(-r_A)$ vs. $X_A$')
plt.grid(True)
# Calculate concentration (C_A) for each X_A value
C_A_values = C_A_in * (1 - X_A_values)
# Plot 1/(-r_A) versus concentration (C_A)
plt.subplot(1, 2, 2)
plt.plot(C_A_values, inv_neg_r_A)
plt.xlabel('Concentration of A, $C_A$ (mol/L)')
plt.ylabel('$1/(-r_A)$')
plt.title('Graphical Representation of $1/(-r_A)$ vs. $C_A$')
plt.grid(True)
plt.tight_layout()
plt.show()Output:

Example Problem on MFR/CSTR
Enzyme E catalyses the fermentation of substrate A (the reactant) to product R. Find the size of mixed flow reactor needed for 95% conversion of reactant in a feed stream (25 liter/min) of reactant (2 mol/liter) and enzyme. The kinetics of the fermentation at this enzyme concentration are given by
A —–> R (Enzymatic Reaction)
Rate of Reaction (mol /liter.min), -rA = 0.1 CA / 1 + 0.5 CA
Given:
- conversion for reactant A, \(X_A\) = 0.95
- Volumetric Feed Rate, \(v_0\) = 25 liter/min
- Initial concentration of feed, \(C_{A0}\) = 2 mol/liter
- Volume of Reactor, \(V\) = ?
based on the given information, first we will find \(C_A\)
\( C_A = C_{A0} (1-X_A) \)
\(C_A\) = 2 * (1 – 0.95) = 0.1 mol/liter
Now, putting the value of \(C_A\) into the rate of reaction, \(-r_A\)
\(-r_A\) = (0.1 * 0.1) / (1 + 0.5 * 0.1) = 0.0095238 mol/ liter.min
using, the equation for Mixed Flow Reactor
\(\frac{V}{v_0} = \frac{C_{A0}X_A}{-r_A} \)
\(\frac{V}{25}\) =\(\frac{2}{0.0095238}\) * \(0.95\)
on solving we get, V = 4989.49 liter ~ 5 m3
Therefore, the size of the mixed flow reactor needed for 95% conversion of reactant in a feed stream (25 liter/min) of reactant (2 mol/liter) and enzyme is 5 m3 .
Resources:
- Chemical Reactor Analysis and Design Fundamentals by Rawlings and Ekerdt
- Elements of Chemical Reaction Engineering by Fogler
- “Chemical Reaction Engineering“ by Octave Levenspiel
Disclaimer: The Solver provided here is for educational purposes. While efforts ensure accuracy, results may not always reflect real-world scenarios. Verify results with other sources and consult professionals for critical applications. Contact us for any suggestions or corrections.