Table of Contents
Net Positive Suction Head (NPSH) is the important factor in the performance of pump operations and prevents cavitation. Accurate NPSH calculations are needed to select the right pump and maintaining reliable operations.
When the pressure at the pump suction drops below the liquid’s vapor pressure, vapour bubbles are formed that collapse and cause noise, vibration, and damage. NPSH is required to prevent this situation.
Related: Newton’s Law of Viscosity Calculator – Dynamic Viscosity
Related: Hagen-Poiseuille Equation Calculator / Poiseuille’s Law Solver
NPSH (Net Positive Suction Head)
Net Positive Suction Head (NPSH) is defined as the difference between pump’s inlet stagnation pressure head and the vapor pressure head and it is written as:
NPSH: Absolute Pressure Head at Pump’s Inlet+ Velocity Head – Vapour Pressure Head (absolute units)
\[\text{NPSH} = \frac{P_{\text{total}}}{\rho g} + \frac{v^2}{2g} – \frac{P_{\text{vapor}}}{\rho g}\]
where in S.I units:
- Ptotal is the absolute pressure at the suction (N/m2 or Pa)
- ρ is the density of the fluid (Kg/m3)
- v is the velocity of the fluid (m/s)
- Pvapor is the vapour pressure of the fluid (N/m2 or Pa)
In other words, NPSH is a measure of the pressure energy in a fluid relative to its vapor pressure. It’s an indicator of how much suction pressure is available to a pump to prevent cavitation.
Related: Head Loss or Pressure Loss Calculator using Darcy-Weisbach Equation
Related: Friction Factor Calculator Moody’s Diagram for Smooth and Rough Pipes
NPSH Calculator for Pumps
This NPSH calculator helps user to determine the available Net Positive Suction Head (NPSHa) for a pump system. Input parameters include static suction head (elevation or height of the pump from reservior). friction loss, fluid density and reservior pressure if it is not open to atmosphere.
Based on the user inputs, the calculator then computes the NPSHa and compares it with the required NPSH to check whether cavitation occurs or not.
Note: Use our Head Loss Calculator and Vapour Pressure Calculator for the tems used in the NPSH calculation.
Related: Head Loss or Pressure Loss Calculator using Darcy-Weisbach Equation
Related: Antoine Equation Calculator for Vapour Pressure versus Temperature Calculations
What is Cavitation and its Cause?
When a liquid is pumped, the pressure inside the pump can drop below the liquid’s vapour pressure (Pv), causing the liquid to boil locally and form vapor bubbles. These bubbles move to the high pressure area in the pump and collapses, this phenomenon is known as Cavitation.

This formation and collapse of bubbles leads to noise, vibration, reduced efficieny and damage to the impeller blades. Major causes of cavitation are:
- Excessive pump speed can increase pressure drops on the suction side.
- Warmer liquids have higher vapor pressures, making cavitation more likely.
- Insufficient pressure at the pump’s suction side reduces the local pressure.
Related: 10 Mostly used Dimensionless Numbers in Chemical Engineering
Related: Centrifugal Pump Sizing Calculation – TDH, NPSHa vs Flow Rate curve & Power Required
How to determine NPSH of a Pump?
To ensure proper pump operation and avoid cavitation, the Net Positive Suction Head available must exceed the NPSH required by the pump.
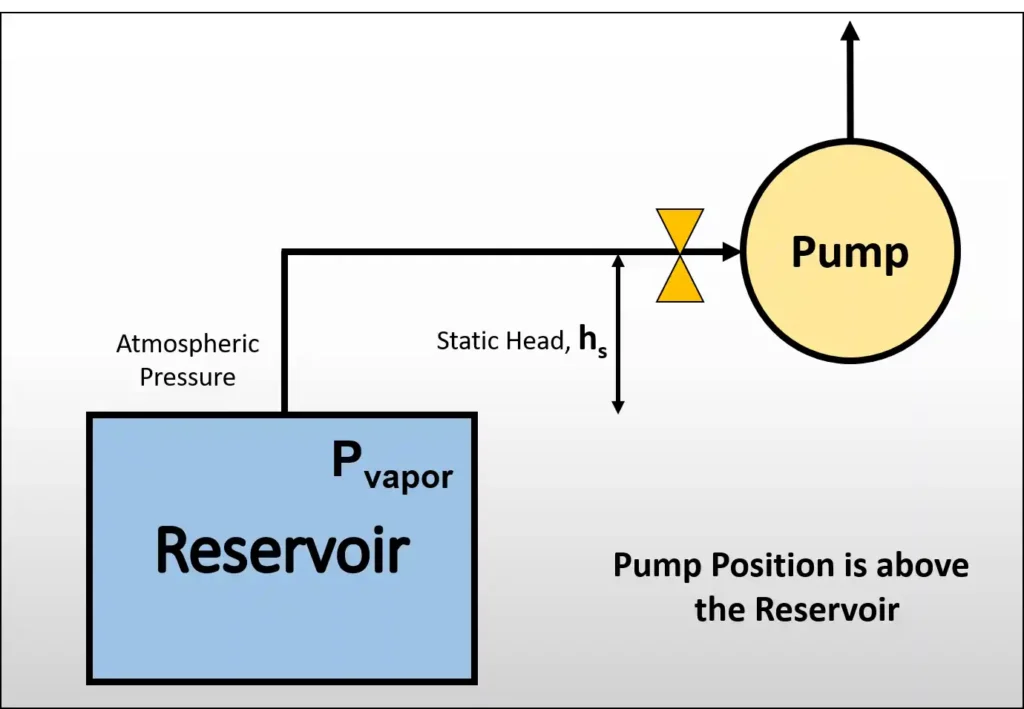
We have already discussed the definition for NPSH. Below is the formula based on practical considerations and Bernoulli’s principle:
\[\text{NPSH}a = \left( \frac{P_{\text{surf}} – P_{\text{vapor}}}{\rho \cdot g} \right) – h_s – H_f \]
Where:
- Surface Pressure, Psurf = Patm + Pres – Here Pres is reservoir’s absolute pressure
- Pvapor is the vapor pressure of the fluid at the given temperature.
- ρ is the fluid density at given temperature.
- hs is the height different between the liquid surface and the pump suction level. This value is negative if the tank is above the pump.
- Hf is the friction head loss due to pipe fittings
Pump manufacturers test pumps and provides net positive suction head required which is the minimum NPSH necessary to avoid cavitation in the pump.
To avoid cavitation NPSHavailable > NPSHrequired i.e (NPSHa > NPSHr)
Related: Hagen-Poiseuille Equation Calculator / Poiseuille’s Law Solver
Example Problem on NPSH Calculation
Calculate the net positive suction head (NPSH) of a centrifugal pump using the following data. Vapour pressure of the liquid = 26.66 kN/m2 . Distance between the level of liquid in the reservoir and suction line = 1.2 m, Density of the liquid = 865 kg/m3 , Friction in the suction line = 3.5 J/kg. Reservoir is open to the atmosphere.
Data Given:
- Density of the Liquid, ρ = 865 Kg/m3
- Friction in the suction line, f = 3.5 J/Kg
- Vapor Pressure of the liquid, Pv = 26660 N/m2
- Static Suction Head (hs) = 1.2 m
- Atmospheric Pressure, Patm = 101325 N/m2
Using formula:
\(\text{NPSH} = \frac{P_{\text{atm}}}{\rho g} – h_s – \frac{P_{\text{vapor}}}{\rho g} – h_f\)
\(\text{NPSH} = \frac{101325 – 26660}{865 \cdot 9.81} – 1.2 – \frac{3.5}{9.81}\)
we get, NPSH = 7.24 m
Related: Reynolds Number Calculator for a Circular Pipe
Related: Fluid Mechanics Calculators
NPSH Calculation using Python Code
This Python code calculates the NPSHa (Net Positive Suction Head Available) for a pump system and compares it with the NPSHr (Required NPSH), and checks for cavitation risk based on user-provided inputs ( pressure, suction head, and reservoir conditions).
Note: This Python code solves the specified problem. Users can copy the code and run it in a suitable Python environment. By adjusting the input parameters, users can observe how the output changes accordingly.
def calculate_npsha(patm, hs, pvapor, hf, density, reservoir_position, reservoir_type, pres=0):
"""
Calculate NPSHa (Available Net Positive Suction Head).
Parameters:
patm (float): Atmospheric pressure in kPa
hs (float): Static suction head in meters
pvapor (float): Vapor pressure in kPa
hf (float): Friction loss in meters
density (float): Fluid density in kg/m^3
reservoir_position (str): 'above' or 'below'
reservoir_type (str): 'open' or 'pressurized'
pres (float): Reservoir pressure in kPa (default 0)
Returns:
float: NPSHa value in meters
"""
# Constants
g = 9.81 # Gravitational acceleration in m/s^2
# Adjust static suction head based on reservoir position
adjusted_hs = hs if reservoir_position == 'above' else -hs
# Convert pressures to head (in meters)
if reservoir_type == 'open':
patm_head = (patm * 1000) / (density * g)
else:
patm_head = (pres * 1000) / (density * g)
pvapor_head = (pvapor * 1000) / (density * g)
# Calculate NPSHa
npsha = patm_head + adjusted_hs - pvapor_head - hf
return npsha
# Sample use case
if __name__ == "__main__":
# Input values (example case)
patm = 101.325 # Atmospheric pressure in kPa
hs = 5.0 # Static suction head in meters
pvapor = 2.0 # Vapor pressure in kPa
hf = 1.5 # Friction loss in meters
density = 1000.0 # Fluid density in kg/m^3
reservoir_position = 'above' # Reservoir position: 'above' or 'below'
reservoir_type = 'pressurized' # Reservoir type: 'open' or 'pressurized'
pres = 200.0 # Reservoir pressure in kPa (only for pressurized type)
npshr = 4.0 # NPSHr (required NPSH) in meters
# Calculate NPSHa
npsha = calculate_npsha(patm, hs, pvapor, hf, density, reservoir_position, reservoir_type, pres)
# Output results
print("NPSHa Calculation:")
print(f"Atmospheric Pressure (P_atm): {patm} kPa")
print(f"Static Suction Head (h_s): {hs} m ({'above' if reservoir_position == 'above' else 'below'} pump)")
print(f"Vapor Pressure (P_vapor): {pvapor} kPa")
print(f"Friction Loss (h_f): {hf} m")
print(f"Fluid Density: {density} kg/m^3")
print(f"Reservoir Type: {reservoir_type}")
if reservoir_type == 'pressurized':
print(f"Reservoir Pressure (P_res): {pres} kPa")
print(f"NPSHa (Available): {npsha:.2f} m")
print(f"NPSHr (Required): {npshr} m")
# Cavitation check
if npsha >= npshr:
print("Result: NPSHa is sufficient. Cavitation will not occur.")
else:
print("Result: NPSHa is insufficient. Cavitation may occur!")Output:
NPSHa Calculation:
Atmospheric Pressure (P_atm): 101.325 kPa
Static Suction Head (h_s): 5.0 m (above pump)
Vapor Pressure (P_vapor): 2.0 kPa
Friction Loss (h_f): 1.5 m
Fluid Density: 1000.0 kg/m^3
Reservoir Type: pressurized
Reservoir Pressure (P_res): 200.0 kPa
NPSHa (Available): 23.68 m
NPSHr (Required): 4.0 m
Result: NPSHa is sufficient. Cavitation will not occur.Resources
- “Fluid Mechanics” by Frank M. White
- “Introduction to Fluid Mechanics” by Robert W. Fox, Alan T. McDonald, and Philip J. Pritchard
- “Principles of Heat and Mass Transfer” by Frank P. Incropera and David P. DeWitt
- Python.org – The official Python website offers tutorials, documentation, and resources for learning Python.
Disclaimer: The Solver provided here is for educational purposes. While efforts ensure accuracy, results may not always reflect real-world scenarios. Verify results with other sources and consult professionals for critical applications. Contact us for any suggestions or corrections.